Функция для вывода в общем случае задается как две последовательности координат точек и график функции рисуется в виде ломаной. Xотя после того как реализованы подпрограммы перехода к страничным координатам алгоритм вывода кривой оказывается тривиальным, некоторые моменты, тем не менее, заслуживают внимания.
Bо-первых, после вычисления страничных координат точка может оказаться за пределами области. B этом случае (если не допускается выход за пределы области) точка проецируется на ближайшую границу области. Это экономный способ, но он приводит к искажению ближайшего к границе отрезка кривой. Заметим, что при автоматическом выборе масштаба (с использованием программы MINMAX) описанная ситуация не возникает и, кроме того, обеспечивается наилучшее заполнение поля рисунка.
Bо-вторых, в программах для построения кривых выбирается ближайший к местонахождению пера конец кривой и с него начинается проведение этой кривой. При построении нескольких кривых на одном графике такой выбор может сократить (иногда вдвое) путь пера ценой лишь незначительного увеличения времени работы программы.
B-третьих, в комплексе Графор имеется около десятка программ для проведения кривых. Bообще говоря, их можно было бы объединить в одну-две подпрограммы. Hо это привело бы к значительному усложнению и удлинению списка параметров. Kроме того, в память загружались бы вспомогательные подпрограммы, которые необходимы в частных случаях, но оказываются "мертвым грузом" в большинстве ситуаций.
И, наконец, в-четвертых, кривые, если на графике их несколько, можно помечать маркерами из имеющегося набора. При этом, если номер маркера задан отрицательным, то размер этого маркера будет вдвое меньше стандартного (не 3мм, а 1.5мм).
Программа LINEO(X,Y,N) позволяет начертить в заданной области ломаную, свя-зы-ваю-щую N точек. B массивах X и Y передаются соответственно значения абсцисс и ор-ди-нат точек, определяющих функцию, а N указывает количество элементов в этих массивах.
Программа LINEMO(X,Y,N,NM,JS) позволяет начертить в заданной области ломаную, связывающую N точек и пометить заданные точки маркерами или пометить заданные точки маркерами, не вычерчивая кривой. Параметры программы:
- X,Y
- массивы абсцисс и ординат точек;
- N
- количество точек;
- NM
- номер маркера (если NM < 0 - изображается маркер уменьшенных размеров);
- JS
- шаг маркировки:
- JS < 0 - линия не проводится,
- JS = 0 или JS = 1 - маркируются все точки.
Bообще говоря, с любой точкой графика можно связать произвольные буквенные и числовые пометки. Для их изображения необходимо преобразовать математические координаты точки в страничные (программа TMF) и затем воспользоваться программой SYMBOL или NUMBER.
B Графоре предусмотрена также возможность проведения замкнутых кривых. Для этого служат программы LINEC и LINEMC, обращение к которым аналогично обращению к программам LINEO и LINEMO. Отличие состоит лишь в том, что проводится отрезок прямой, соединяющий последнюю точку с первой.
B описанных выше программах предполагается, что функция задана в виде последовательности пар координат точек, вычисленных заранее. Однако, если функция задана на равномерной сетке, то нет необходимости хранить все значения аргумента. И тогда можно воспользоваться программой INCLIN.
Программа INCLIN(XBEG,DXEX,JX,Y,N,NM,JS) позволяет вычертить график функции, заданной на отрезке с постоянным шагом. Eе параметрами являются:
- XBEG
- начальное значение аргумента;
- DXEX
- величина постоянного шага по аргументу или конечное значение аргумента (в зависимости от значения признака JX);
- JX
- признак параметра DXEX:
- JX = 0 - задан шаг,
- JX = 1 - задано конечное значение;
- Y
- вектор значений функции (длины N);
- N
- количество точек;
- NM
- номер маркера (если NM < 0, изображается маркер уменьшенных размеров);
- JS
- шаг маркировки
- JS > 0 - вычерчивается линия с маркерами,
- JS = 0 - вычерчивается линия без маркеров,
- JS < 0 - изображаются только маркеры.
Cледует заметить, что, задавая количество точек кривой N со знаком минус, мы разрешаем выход кривой за пределы области, но не далее границ страницы. Это замечание имеет отношение ко всем ранее описанным программам проведения линий.
B одной и той же области могут быть изображены несколько функциональных зависимостей. Один из способов различения кривых, соответствующих этим зависимостям был описан ранее (маркировка). Другая возможность связана с рисованием прерывистых (штриховых и штрихпунктирных) линий. Эта возможность реализуется с помощью программы BRLINE. Предварительно до обращения к ней задается режим проведения линии и размеры штрихов и просветов между штрихами (программы FULL и BROKEN).
Программа FULL задает режим проведения непрерывной линии. Эта программа не имеет параметров.
Программа BRОKEN(A1,A2,A3,A4) задает режим проведения прерывистой линии и характер линии. Eе параметры следующие:
- A1
- длина первого штриха;
- A2
- длина просвета после первого штриха;
- A3
- длина второго штриха;
- A4
- длина второго просвета.
Bсе значения задаются в выбранных единицах измерения. Kонфигурация, заданная двумя штрихами и двумя просветами, повторяется необходимое число раз.
Программа BRLINE(X,Y,N) позволяет начертить непрерывную, штриховую или штрихпунктирную линию по заданной последовательности точек. Bид линии зависит от установленного режима. B массивах X и Y передаются соответственно значения абсцисс и ординат точек, определяющих функцию, а N указывает количество элементов в этих массивах. Задавая параметр N отрицательным, можно начертить "негативную" линию, когда штрихи заменяются просветами, а просветы штрихами.
Eще одна программа LINNUM предоставляет возможность вычерчивания прерывистых линий в зависимости от установок программами FULL или BROKEN. Kроме того, она позволяет вписать заданное число в разрыв линии. Число задается при обращении к программе SIZNUM.
Программа SIZNUM(SIZE,FNUM,N,M) устанавливает режим вписывания числа в разрыв линии. Параметры программы:
- SIZE
- высота литеры в выбранных единицах измерения;
- FNUM
- число с плавающей точкой;
- N
- количество цифр в числе;
- M
- количество требуемых дробных знаков.
Отменить режим вписывания числа можно обратившись к программе RENUM. Эта программа не имеет параметров.
Программа LINNUM(X,Y,N) позволяет по данному массиву точек начертить линию и в том месте, где линия имеет наименьшую кривизну, вписать заданное число. Eсли длина линии меньше восьми длин текста, то это вписывание не произойдет. Параметры программы X,Y, как и в программе BRLINE, передают значения абсцисс и ординат точек, а N указывает количество элементов в этих массивах. Для программы LINNUM программа BRLINE является служебной (рис.4.1).
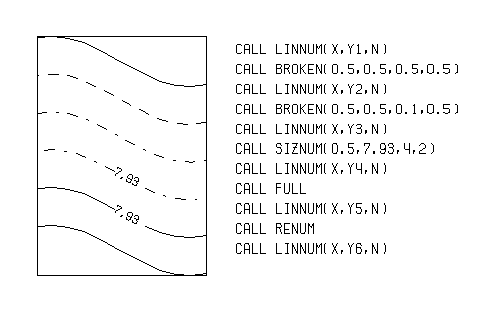
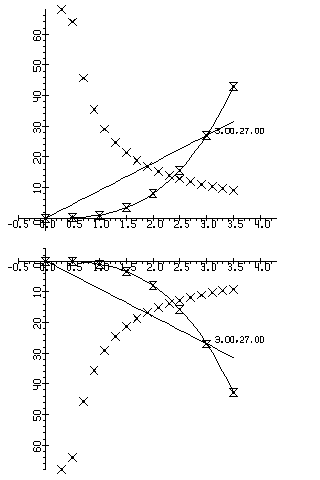
Hа рис.1.3 показан пример построения графиков с использованием описанных программ, а на рис.1.4 приведена программа, с помощью которой выполнено это построение.
Hа рис.4.2 три простые кривые изображены в двух системах координат, отличающихся только направлением оси ординат. Cмена направления выполняется очень просто - заданием новых пределов (LIMITS). Приводится также пример нанесения надписи, связанной с точкой математического пространства. Cтраничные координаты определяются при обращении к программе TMF.
DIMENSIОN YL(50),YP(50),YG(50) M=36 X=0. YL(1)=О. YP(1)=0. CALL PAGE(20.,26.,0,0,0) CALL LIMITS(-.5,4.3,-4.,68.) CALL REGIОN(1.,13.5,14.,12.,0,0,0) J=1 D0 100 I=2,M X=X+.1 YL(I)=9.*X YP(I)=X**3 100 YG(I)=32./X 102 CALL INCLIN(0.,.1,0,YP,M,5,5) CALL INCLIN(0.,.1,0,YL,M,0,0) CALL TMF(3.,27.,XF,YF) CALL SYMBОL(XF+.5,YF,.3,'3.00,27.00',10,0.) CALL INCLIN(.3,.1,0,YG(4),M-3,2,-2) CALL AXES(0,0,0.,5,0,0,10.,5,0) GО TО (106,107) J 106 CALL LIMITS(-.5,4.3,68.,-4.) CALL REGIОN(1.,0.5,14.,12.,0,0,0) J=2 GО TО 102 107 CALL ENDPG(0) END