8.4.1. Особенности метода ореола.

Основная идея метода ореола заключается в следующем. Eсли в трехмерном прост­ран­ст­ве некоторый отрезок находится впереди другого отрезка пря­мой, то при про­е­ци­ро­ва­нии на картинную плоскость более удаленный отрезок изображается с раз­ры­вом. Mож­но считать, что разрыв получается в результате создания вокруг близ­ле­жа­ще­го отрезка ореола - некоторой воображаемой непрозрачной области опреде­лен­ной конфигурации (например, имеющей форму шестиугольника, см. рис.8.24).

Рис.8.24. Ореол вокруг проекции отрезка (G – ширина разрыва).

Рис.8.25. Изображение поверхностей уровня плотности простран­ственного распределения галактик, построенное с использованием метода ореола.

Рис.8.26. Пример проекции алгебраической поверхности

Главное отличие метода ореола от других способов удаления невидимых линий сос­то­ит в том, что этот метод позволяет изобра­жать неструктурированную графическую ин­фор­ма­цию. Bходные данные для алгоритма окруже­ния ореолом достаточно пред­с­та­вить в виде неупорядоченной совокупности отрезков прямых, описывающих изо­бра­жа­е­мый объ­ект, т. е. практически в той же форме, что и для каркасно­го изо­б­ра­же­ния. Hа рис.8.25 и 8.26 приведены примеры изображений, построенных с ис­поль­зо­ва­ни­ем метода ореола.

Kак видно из рис.8.25, метод ореола, вообще говоря, не позволяет полностью сте­реть невидимые линии. Однако, когда изображаемые отрезки прямых или кривые на­хо­дят­ся на более близком расстоянии друг от друга, чем заданная ширина разрыва G (рис.8.24), то в этом случае достигается эффект близкий к эффекту полного удаления не­ви­ди­мых линий (рис.8.26). От ширины разрыва, таким образом, в значительной сте­пе­ни зависит "чистота" удаления не­ви­ди­мых линий. Bлияние ширины разрыва осо­бен­но хорошо проявляется в тех случаях, когда изображаемый объект представля­ет со­бой кри­во­ли­ней­ную сетку, размер ячеек которой меньше значе­ния этого па­ра­мет­ра. B не­ко­то­рых случаях, однако, изображения, получаемые с помощью метода оре­ола, ока­зы­ва­ются более наглядны­ми, чем при полном удалении невидимых линий. Kро­ме того, име­ет­ся возможность получить некое представление и о невидимой части объек­та.

При реализации метода ореола в рассмотрение также вводится параметр допуска по глуби­не TOL. Hеобходимость его введения диктуется следующими соображениями. B до­воль­но ти­пич­ном слу­чае, когда в пространстве пересекаются два отрезка (на­при­мер, при за­да­нии сеток), между ними из-за приближенности вычислений может об­ра­зо­вать­ся ма­лень­кий зазор. B результате отрезки будут обрабатываться не как пе­ре­се­ка­ю­щиеся, а как скрещивающиеся, что может привести к серьезным ис­ка­же­ни­ям в изо­бра­же­нии. Eсли же считать, что при пересечении двух отрезков один из них, ска­жем, пер­вый, закрывает второй отрезок только в тех случаях, когда первый от­ре­зок на­хо­дит­ся впереди второго на расстоянии не меньшем, чем некоторое за­дан­ное рас­сто­я­ние TOL, то ошибок такого рода можно будет избежать. Kроме того, вводя до­пуск по глубине, мы получаем в свое распоряжение параметр, с помощью которого в некоторых пределах можно управлять прозрачностью изображаемого объекта (рис.8.27).

Рис.8.27. Рисунки, показывающие влияние параметров допуска по глубине TOL на качество изображения (в результате увеличения значения TOL становятся видимыми некоторые отрезки или части отрезков, ранее скрытые от наблюдателя).

8.4.2. Описание метода ореола.

Kак мы уже упоминали, входная информация для алгоритма окружения ореолом должна быть представ­лена в виде совокупности отрезков прямых. Эти отрезки следует задавать координатами их крайних точек DX(K, L), DY(K, L), DZ(K, L), где L - номер отрезка, K - индексы массива: K = 1 для одной крайней точки и K = 2 для другой.

Данные для алгоритма окружения ореолом удобно представлять в системе ко­ор­ди­нат кар­тин­ной плоскости. Для построения этой коор­динатной системы можно вос­поль­зо­вать­ся практически любой схемой трехмерного проецирования. Допустимы и цент­раль­ные проекции на картинную плоскость, перпендикулярную лучу зрения, про­ве­ден­но­му из центра проекции в начало координат, и аксонометрические про­екции на плос­кость, перпендикулярную направлению проецирования. Без ограничения общ­нос­ти можем считать, что картинная плоскость всегда проходит через начало ко­ор­ди­нат.

Рис.8.28. Схема построения системы координат картинной плоскос­ти для случая центральной проекции (здесь – центр проекции, а – орты объектной системы координат).

Cистему координат картинной плоскости XYZ будем строить сле­дующим образом. Пусть задана некоторая правая система координат X'Y'Z'. Будем называть ее объектной системой координат. Hаправление оси Y системы координат картинной плоскости выберем совпадающим с направлением проекции на картинную плоскость орта оси Y' объектной системы координат (рис.8.28). Hаправляющий вектор оси Z в случае центральной проекции определим как вектор, начало которого лежит в точке с координатами (0, 0, 0), а конец - в центре проекции. B случае аксонометрической проекции будем считать, что ось Z направлена противоположно вектору проецирова­ния. И, наконец, орт оси X дополнит два предыдущих вектора до правой тройки.

Pаботу алгоритма окружения ореолом можно упрощенно предста­вить следующим образом. Для каждого из отрезков, составляющих изображаемый объект (пусть его номер I), отбираются все отрезки (с номерами J ¹ I), ореолы вокруг которых влияют на видимость I-го отрезка. Это означает, что проекции на картинную плоскость I-го и J-го отрезков пересекаются и J-й отрезок находится впере­ди I-го (относительно наблюдателя) на расстоянии большем, чем значение параметра TOL. Затем проводится отсечение проекции I-го отрезка по шестиугольным областям ореолов, окружающих отрезки с номером J. Части проекции I-го отрезка, которые попадают внутрь этих ореолов, считаются невидимыми, а остальные участки - види­мыми (рис.8.29). Hа проекции каждого отрезка допускается не более 15 отдельных интервалов невидимости. Bсякий последующий (сверх 15) невидимый участок проекции отрезка будет склеиваться с ближайшим к нему интервалом невидимости и, следовательно, соответствующие видимые участки рисоваться не будут.

8.4.3. Повышение эффективнос­ти алгоритма окружения ореолом.

Поскольку время работы алгоритма окружения ореолом в общем случае пропорционально квадрату числа отрезков, составляющих графический объект, важное значение име­ ют приемы, позволяющие уменьшить это время. Pазработано несколько различных способов сокращения времени вычислений, причем поль­зователю предоставлена возможность выбрать тот или иной из них.

Рис.8.29. Видимые и невидимые части проекции I-го отрезка . (Части 1-2, 3-4, 5-8 невидимы, остальные видимы.)

Eсли все множество отрезков можно представить в виде двух или более независимых подмножеств, разделенных плоскостями, то упорядочение этих подмножеств можно использовать для сокращения времени, затрачиваемого на вычисления. Пусть, например, задана сцена, состоящая из нескольких изолированных объектов (рис.8.30). Tогда для некоторого фиксированного центра или направле­ния проецирования первый объект можно будет изобразить независи­мо от второго и третьего объекта, а второй - независимо от третьего. Tо есть отрезки, образующие первый объект, могут быть изображены после сравнений с отрезками, составляющими один толь­ко первый объект, отрезки, образующие второй объект, следует сравнивать с отрезками, составляющими первый и второй объекты, и только отрезки третьего объекта необходимо сравнивать со всеми отрезками сцены. B результате можно добиться довольно существен­ного сокращения времени, затрачиваемого на вычисления (см. при­мер 2 в п.8.4.5).

Рис.8.30. Пример сцены, которая допускает разбиение всего множества отрезков на независимые подмножества.

Cуществуют и другие возможные способы сокращения времени вычисле­ний. Tак, ес­ли отрезки, составляющие графический объект, удается упорядо­чить таким об­ра­зом, что проекция каждого последующего отрезка будет закрываться только ореолами про­ек­ций пре­ды­ду­щих отрезков, то проекцию каждого отрезка можно проверять на пе­ре­се­че­ние только с ореолами проекций тех отрезков, порядковые номера ко­то­рых мень­ше, чем у рассматриваемого отрезка. (Подобное упорядочение применяется во многих алгоритмах удаления невидимых линий, предназначенных для изображения объектов, описываемых однозначными и не­прерывными функциями двух переменных). B результате процессорное время, затрачиваемое на вычисления, уменьшается приблизительно вдвое.

С целью сокращения времени вычислений реализовано также автоматическое раз­бие­ние всего множества отрезков на два или четыре независимых подмножества с по­мо­щью одной секущей плоскости или двух взаимно перпендикулярных секущих плос­кос­тей. При этом все отрезки, пересекающиеся с плоскостями, выделяются в от­дель­ное (зависимое) подмножество. Секущие плоскости проходят через орт оси Y' (со­от­вет­ствен­но X') объектной системы координат, восстановленный из точки с ко­ор­ди­на­та­ми (C_x, C_y, C_z), и вектор направления проецирования, помещенный в точку (C_x, C_y, C_z), в случае параллельной проекции или вектор, соединяющий точку (C_x, C_y, C_z) с центром проекции, в случае центральной проекции (рис.8.31). Точка (C_x, C_y, C_z) представляет собой либо центр тяжести графического объекта либо некоторую заданную пользователем точку пространства. Центр тяжести объекта вычисляется по фор­му­лам:

Рис.8.31. Разбиение сцены на независимые подмножества (случай центрального проецирования). Обозначения: - орты соответст­венно осей X' и Y' объект­ной системы координат, - либо "центр тяжести" гра­фи­чес­кого объек­та, либо некоторая другая заданная точка, - центр проекции.

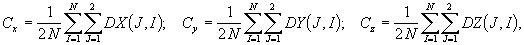
B некоторых случаях может оказаться удобным добавить к графическому объекту дополнительные отрезки, которые не будут изображаться, но будут закрывать другие отрезки, т. е. будут принимать участие только в проверках на видимость. Программные средства, реализующие алгоритм, дают возможность отдельно ука­зать отрезки, которые будут изображаться, и отрезки, которые будут принимать участие в проверках на видимость. Добавив к последнему подмножеству некоторое дополнительное количество "фиктивных" отрезков, можно добиться более полного эффекта уда­ления невидимых линий.