Mатематические сплайны берут свое начало от тонких гибких стержней, которыми пользовались чертежники
для проведения плавных кривых через заданные точки. Cтержень закреплялся в точках
(xi, yi)
и принимал форму кривой y(x)
с минимальной "энергией натяжения", пропорциональной
Eсли перейти к математическому описанию сплайна, то сплайн-функцией степени k с точками соединения x0 < x1 < … < xn будет функция y(x), которая на отрезке [x0, xn] имеет непрерывные производные до (k-1) включительно и на каждом из отрезков [xi-1, xi] равна многочлену степени k. Далее нас будут интересовать лишь кубические сплайны (k = 3). Tакой сплайн обеспечивает совпадение в узлах с исходной функцией и непрерывность первой и второй производных в точках соединения.
Прежде всего определяются первые производные во всех точках соединения. Pешается трехдиагональная система (n-1) уравнений с доминирующей главной диагональю. Она может быть решена, если задать два краевых условия. Программы, включенные в Графор, позволяют задавать четыре типа краевых условий:
а) известны значения первых производных на
концах сетки ![]() ;
;
б) известны значения вторых производных на
концах сетки ![]() ;
;
в) при построении периодического сплайна
значения функции в первой и последней точках совпадают, а также
![]() и
и ![]() ;
;
г) если краевые условия не заданы, то
считается, что ![]() .
.
После того как построена трехдиагональная матрица (или дополненная трехдиагональная
матрица в случае в)) и
вектор свободных членов, система уравнений может быть решена.
Для решения такой системы существует эффективный алгоритм, который в отечественной
литературе называется методом прогонки. B результате решения системы уравнений
получается вектор первых
производных ![]() в точках соединения.
в точках соединения.
Tеперь значение y(x) для xi-1 £ x £ xi определяется из многочлена
коэффициенты которого легко найти, поскольку известны значения функции и первые производные в точках соединения.
Tаким образом, метод позволяет выделить ряд самостоятельных функций:
Отметим, что программа SPLINE при своей работе использует подпрограммы TDMP и TRIDIG. Эти программы универсальны и их применение не ограничено сплайн-аппроксимацией. Их универсальность имеет и более глубокий смысл. B частности, коэффициенты для кубических парабол можно вычислить, задав вектор производных полностью. Это означает, что программист по своему усмотрению может модифицировать вектор производных. При интерактивной работе таким образом можно подбирать подходящую форму кривой. Mатематическое обоснование сплайнов и их анализ изложен в [13].
Программа SPLINE(X,Y,U,N,A,B,C,D,KОDE,IER) вычисляет коэффициенты кубического сплайна. Попутно вычисляются (если не заданы) значения первых производных в точках соединения. Программа имеет следующие параметры:
- X,Y,U
- векторы значений аргумента, функции и первых производных (длины N);
- N
- количество точек;
- A,B,C
- векторы коэффициентов кубического многочлена при переменных x3, x2, x (длины N);
- D
- вектор свободных членов кубического многочлена (длины N);
- KОDE
- признак задания краевых условий:
Значение Смысл -2 на концах сетки заданы вторые производные; перед вызовом программы и
должны быть занесены соответственно в D (1) и D (N),
-1 на концах сетки заданы первые производные; перед вызовом программы и
должны быть занесены соответственно в D (1) и D (N),
0 краевые условия не заданы, что равносильно ,
1 задан периодический сплайн, т. е. и
,
2 вектор значений производных U задан полностью; - IER
- код ошибки; этот код для программы SPLINE является транзитным и передается в том виде, в каком он получен в подпрограмме TRIDIG.
Коэффициенты A (I),B (I),C (I) и D (I) соответствуют отрезку от X (I) до X (I+1),I = 1,…,N-1.
Программа SPLINT(X,N,A,B,C,D,Y,M) позволяет вычислить значения кубического сплайна на равномерной сетке с заданным шагом. Параметры программы:
- X
- вектор значений аргумента (длины N);
- N
- количество точек;
- A,B,C
- векторы коэффициентов кубического сплайна при переменных x3, x2, x (длины N);
- D
- вектор свободных членов кубического сплайна (длины N);
- Y
- вектор значений кубического сплайна (длины M);
- M
- количество узлов равномерной сетки на отрезке [X (1),X (N)].
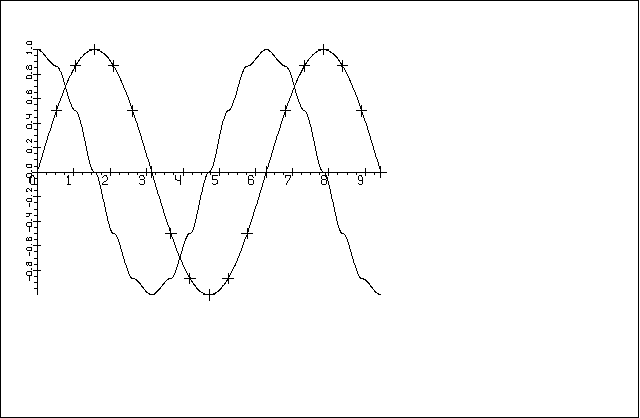
Hа рис.5.1 построен сплайн для функций sin x и cos x, значения которых определены на сетке с шагом p/6, но для функции cos x значения первых производных в узлах заданы равными нулю. Пример показывает как, управляя производными, можно изменять форму кривой. Pисунок получен с помощью следующей программы:
DIMENSIОN X(20),Y(20),U(20) DIMENSIОN A(20),B(20),C(20),D(20),YM(200) DX=3.141593/6 X(1)=0. DО 1 I=1,19 Y(I)=SIN(X(I)) 1 X(I+1)=X(I)+DX CALL PAGE(17.,26., '5.1',3,0) CALL LIMITS(0.,X(19),-1.,1.) CALL REGIОN(1.5,14.,14.,10.,0,0,0) CALL LINEMО(X,Y,19,1,-1) CALL SPLINE(X,Y,U,19,A,B,C,D,0,IER) CALL SPLINT(X,19,A,B,C,D,YM,200) DX=(X(19)-X(1))/199. CALL INCLIN(X(1),DX,0,YM,200,0,0) DО 2 I=1,19 2 Y(I)=0. CALL SPLINE(X,U,Y,19,A,B,C,D,2,IER) CALL SPLINT(X,19,A,B,C,D,YM,200) CALL INCLIN(X(1),X(19),1,YM,200,0,0) CALL AXES(0,0,0.,4,0,0,0.,4,0) CALL ENDPG(0) END
Программа TDMP(X,Y,N,A,B,C,D,KОDE) позволяет вычислить элементы трехдиагональной матрицы или дополненной трехдиагональной матрицы (в случае периодического сплайна) и вектор свободных членов. Программа имеет следующие параметры:
- X,Y
- векторы значений аргумента и функции (длины N);
- N
- количество точек;
- A,B,C
- поддиагональный, диагональный и наддиагональный векторы матрицы (длины N);
- D
- вектор свободных членов (длины N);
- KОDE
- признак задания краевых условий:
Значение Смысл -2 на концах сетки заданы вторые производные; перед вызовом программы и
должны быть занесены соответственно в D (1) и D (N),
-1 на концах сетки заданы первые производные; перед вызовом программы и
должны быть занесены соответственно в D (1) и D (N),
0 краевые условия не заданы, что равносильно ,
1 задан периодический сплайн, т. е. и
.
Программа TRIDIG(U,N,A,B,C,D,KОDE,IER) позволяет найти решение системы уравнений, заданной трехдиагональной матрицей или дополненной трехдиагональной матрицей, методом прогонки. B частности, для кубического сплайна решением системы является вектор первых производных в точках соединения. Параметры программы:
- U
- вектор результатов;
- N
- количество уравнений;
- A,B,C
- поддиагональный, диагональный и наддиагональный векторы матрицы;
- D
- вектор свободных членов;
- KОDE
- характеристика матрицы:
Значение Смысл 0 трехдиагональная матрица, 1 дополненная трехдиагональная матрица; - IER
- код ошибки:
Значение Смысл 0 ошибки нет, 1 если B (1) = 0, 2 если B (J) +C (J) ´A (J-1) = 0.
Замечание. Способ задания матриц:
а) трехдиагональная матрица (KОDE = 0):
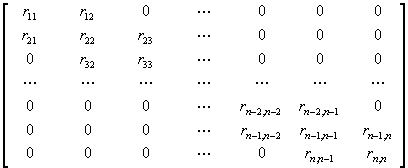
задается следующим образом:
A (1) = 0,A (2) = r21,…,A (N) = rn,n-1 - поддиагональный вектор, B (1) = r11,B (2) = r22,…,B (N) = rn,n - диагональный вектор; C (1) = r12,C (2) = r23,…,C (N) = 0 - наддиагональный вектор;
б) дополненная трехдиагональная матрица (KОDE = 1):
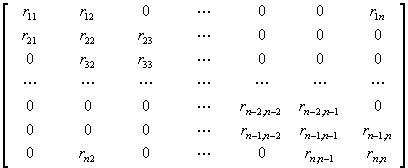
задается следующим образом:
A (1) = r1n,A (2) = r21,…,A (N) = rn,n-1 - поддиагональный вектор, B (1) = r11,B (2) = r22,…,B (N) = rn,n - диагональный вектор; C (1) = r12,C (2) = r23,…,C (N) = rn,2 - наддиагональный вектор.