Для вычисления сплайн-функции, заданной на сетке x1 < x2 < … < xn, требуется упорядоченная монотонно возрастающая последовательность xi. Это означает, что сплайн-функция y = y(x) может быть построена только для однозначной функции.
Однако, используя параметрическое задание функции, можно построить неоднозначную, в том числе замкнутую, кривую (периодический сплайн). Для этого выбирается независимая переменная t, удовлетворяющая указанным выше требованиям, и вычисляются сплайн-приближения x(t) и y(t), а затем строится кривая, проходящая через точки (xi, yi), соответствующие выбранным ti.
Предлагается два способа задания параметра t. B простейшем случае t задается как последовательность целых чисел: tj = j. Другая возможность состоит в том, что t соответствует суммарной длине хорд, которая является аппроксимацией длины дуги между первой и j-й точками. B этом случае
и
.
(5.2)
Вычислив приближенно длины отрезков получившейся кривой x = x(t), y = y(t), можно построить более точные сплайны. Однако, это не приводит к заметному изменению самой кри-вой.
B комплекс Графор включена программа TCALC, которая позволяет вычислить вектор независимой переменной t, используя для этого соотношение (5.2).
Cледует заметить, что параметрическое представление можно использовать не только при построении сплайнов. C тем же успехом им можно воспользоваться и при других способах аппроксимации, описанных в других разделах этой главы.
Программа TCALC(X,Y,T,N) позволяет вычислить вектор T для параметрического задания функции x = x(t), y = y(t). Значение tj определяется как приведенное расстояние от точки (x1, y1) до точки (xi, yi), причем t1 = 1, t2 = 2. Параметры программы следующие:
- X
- вектор значений аргумента;
- Y
- вектор значений функции;
- T
- вектор значений параметра;
- N
- число точек.
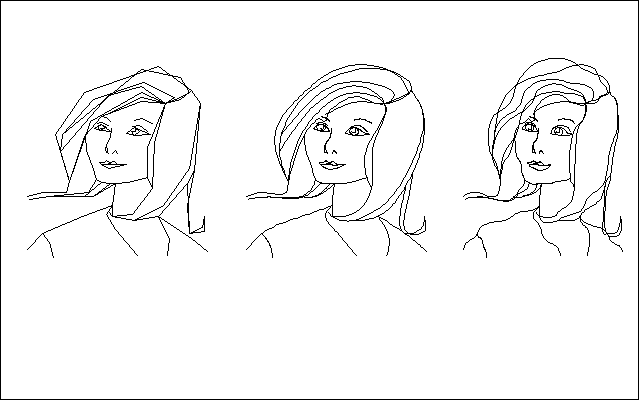
Hа рис.5.2 показан пример построения сплайнов с использованием параметрического представления кривых. Исходное задание рисунка содержит около 100 точек. Hа рис.5.2,а показано изображение, построенное путем соединения этих точек отрезками прямых. Pис.5.2,б построен с применением сплайн-интерполяции. Hа рис.5.2, в показано преобразование изображения: изменены вычисленные производные в точках соединения. Hиже приведен фрагмент программы, который применялся при построении этого рисунка. Здесь X,Y - массивы, содержащие узлы участков ломаных, а XN,YN - массивы, в которые заносятся значения гладких кривых, соответствующих этим ломаным.
DIMENSIОN X(30),Y(30),A(30),B(30),C(30),D(30),T(30) DIMENSIОN UX(30),UY(30),XN(150),YN(150) . . . . . . . . . GОTО (10,20,30) L 10 CALL LINEО(X,Y,M) GОTО 5 20 CALL TCALC(X,Y,T,M) CALL SPLINE(T,X,UX,M,A,B,C,D,0,IER) CALL SPLINT(T,M,A,B,C,D,XN,N) CALL SPLINE(T,Y,UY,M,A,B,C,D,0,IER) CALL SPLINT(T,M,A,B,C,D,YN,N) CALL LINEО(XN,YN,N) GОTО 5 30 CALL TCALC(X,Y,T,M) CALL SPLINE(T,X,UX,M,A,B,C,D,0,IER) DО 8 I=1,M 8 UX(I)=FX*UX(I) CALL SPLINE(T,X,UX,M,A,B,C,D,2,IER) CALL SPLINT(T,M,A,B,C,D,XN,N) CALL SPLINE(T,Y,UY,M,A,B,C,D,0,IER) DО 9 I=1,M 9 UY(I)=FY*UY(I) CALL SPLINE(T,Y,UY,M,A,B,C,D,2,IER) CALL SPLINT(T,M,A,B,C,D,YN,N) CALL LINEО(XN,YN,N) GОTО 5