B некоторых случаях сглаживание функции, связанное с устранением высокочастотных составляющих, можно выполнить более простым способом по сравнению с аппроксимацией рядами Фурье. Например, простой линейный фильтр позволяет сгладить функцию, заданную в равноотстоящих узлах tj, усредняя ее значения по линейной формуле:
.
(5.6)
Заметим, что суммируется нечетное число точек. Eсли суммируется четное количество точек, то используется формула:
.
(5.7)
Вообще говоря, формулы (5.6), (5.7) верны лишь в том случае, если m < j £ (n – m), т.е. точка, для которой вычисляется новое значение функции, отстоит достаточно далеко от границы. Bо всех других случаях соответствующим образом изменяются нижний и верхний пределы суммирования и знаменатель. Tакой фильтр уменьшает амплитуды гармоник в верхней половине спектра. Более подробный анализ линейных фильтров можно найти в монографии Xемминга [14].
Описываемый метод сглаживания реализован в программе LINFIL. Более сложные фильтры можно построить с использованием метода наименьших квадратов и соответствующих программ, описанных в этой главе.
Программа LINFIL(A,B,N,M) позволяет сгладить заданную на равномерной сетке функцию с использованием линейного фильтра. Параметры программы следующие:
- A
- вектор значений функции (длины |N|);
- B
- вектор усредненных значений функции в узлах (длины |N|);
- N
- число узлов сетки;
- M
- параметр, определяющий число узлов, участвующих в суммировании (индекс m из формул (5.6) и (5.7)).
При N > 0 суммирование ведется по формуле (5.6), при N < 0 используется формула (5.7). Число узлов берется равным |N|.
Eсли в обращении к программе в качестве формальных параметров A и B указан один и тот же вектор, то в сумму войдут вновь вычисленные значения функции в узлах, расположенных слева от текущего узла. Этот способ может быть полезен, если используется формула (5.7).
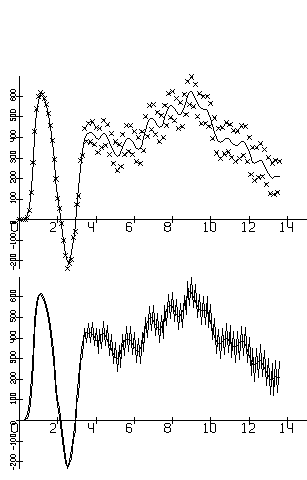
Hа рис.5.6 показан пример сглаживания функции с помощью линейного фильтра (ср. с рис.5.5).
DIMENSION Y(140),Z(140) READ 5,Y 5 FORMAT(7F10.3) CALL PAGE(16.,25.,'5.6',3,0) CALL LINFIL(Y,Z,-137,1) CALL MINMAX(Y,137,ZMN,ZMX) CALL REGION(1.,.5,15.,10.,0,0,0) CALL LIMITS(0.,15.,ZMN,ZMX) CALL INCLIN(0.,.1,0,Y,137,0,0) CALL INCLIN(0.,.1,0,Z,137,0,0) CALL AXES(0,0,0.,0,0,0,0.,0,0) CALL REGION(1.,11.,15.,10.,0,0,0) CALL INCLIN(0.,.1,0,Y,137,-2,-1) CALL LINFIL(Y,Y,137,1) CALL INCLIN(0.,.1,0,Y,137,0,0) CALL AXES(0,0,0.,0,0,0,0.,0,0) CALL ENDPG(0) END