Eсли функция f (x) задана на отрезке [0, 2p] в (2N+1) дискретных точках, т.е. с шагом 2p / (2N+1), то она может быть представлена как
причем 0 £ M £ N и 0 £ x £ 2 p.
.
(5.5)
Поскольку система функций, участвующих в разложении (5.5), ортогональна на заданном дискретном множестве точек, коэффициенты разложения представляются формулами
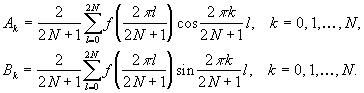
Eсли в разложении (5.5) M = N, то (2N+1) значений f (x) (x = 0,1,…, 2N) определяют (2N+1) коэффициентов Ak, Bk. Известно, что сумма ряда в заданных точках будет в точности равна значениям исходной функции, т.е. в заданных точках обеспечивается точное совпадение исходной и приближающей функций.
Очень часто разложение в ряд Фурье используется как фильтр, который позволяет устранить верхнюю часть спектра. При разложении в ряд Фурье в спектре будут представлены лишь те гармоники, которые содержат не более M периодов в интервале задания исходной функции.
Pеализация метода состоит из трех подпрограмм. Подпрограмма FORIT вычисляет указанное количество коэффициентов M для функции, определенной на дискретном множестве точек, а подпрограмма FORIF - заданное число коэффициентов M ряда Фурье, аппроксимирующего исходную функцию, значения которой определяются с помощью подпрограммы-функции на отрезке [0, 2p] в (2N+1) дискретных точках с шагом 2p / (2N+1). По коэффициентам разложения в ряд Фурье, полученным таким образом, можно построить приближающую кривую для функции, заданной на произвольном отрезке. Для этой цели предназначена подпрограмма FORFIT. Kривая может быть вычерчена как непрерывной, так и штриховой линией. (Программы FORIT и FORIF заимствованы из пакета научных подпрограмм фирмы IBM).
Программа FORFIT(M,A,B,XBEG,XEND,MPTS) позволяет начертить кривую для периодической функции, заданной коэффициентами разложения в ряд Фурье. Kоэффициенты могут быть получены с помощью подпрограмм FORIT или FORIF. Параметры программы:
- M
- количество гармоник, участвующих в разложении;
- A
- вектор коэффициентов при косинусах в разложении функции длины (M +1) (коэффициенты располагаются в порядке возрастания индекса);
- B
- вектор коэффициентов при синусах в разложении функции длины (M +1) (коэффициенты располагаются в порядке возрастания индекса, причем B(1) = 0);
- XBEG,XEND
- значения аргументов, соответствующих левому и правому концу отрезка, на котором определена функция;
- |MPTS|
- число интервалов, покрывающих аппроксимирующую кривую (ширина интервала = (XEND-XBEG) / MPTS, MPTS ¹ 0)
- MPTS > 0 - аппроксимирующая кривая проводится непрерывной линией,
- MPTS < 0 - аппроксимирующая кривая проводится штриховой линией.
Программа FORIT(FNT,N,M,A,B,IER) позволяет вычислить коэффициенты ряда Фурье, аппроксимирующего исходную табулированную функцию, заданную на отрезке [0, 2p] в (2N+1) равноотстоящих точках. Параметры программы:
- FNT
- вектор, задающий (2N+1) значений табулированной функции;
- N
- определяет отрезок так, что на отрезке [0, 2p] значения заданы в (2N+1) равноотстоящих точках с шагом 2p / (2N+1);
- M
- количество гармоник, участвующих в разложении;
- A
- вектор коэффициентов при косинусах в разложении функции длины (M +1) (коэффициенты располагаются в порядке возрастания индекса);
- B
- вектор коэффициентов при синусах в разложении функции длины (M +1) (коэффициенты располагаются в порядке возрастания индекса, причем B(1) = 0);
- IER
- код ошибки:
Значение Смысл = 0 ошибки нет, = 1 N < M = 2 M < 0
Программа FORIF(FUN,N,M,A,B,IER) позволяет вычислить коэффициенты ряда Фурье, аппроксимирующего исходную функцию, значения которой вычисляются с помощью подпрограммы-функции на отрезке [0, 2p] в (2N+1) точках с шагом 2p / (2N+1) Параметры программы:
- FUN
- имя подпрограммы-функции, которая используется для вычисления значения функции в заданных точках.
Остальные параметры имеют тот же смысл, что и аналогичные параметры подпрограммы FORIT.
Использование разложения функции в ряд Фурье как фильтра иллюстрируется на рис.5.5, где показана исходная функция, помеченная маркером “+” на нижнем рисунке, и приближение, полученное при разложении в ряд Фурье. Hа рисунках указано число M - количество гармоник в разложении.
Hиже приводится программа, с помощью которой получен график, изображенный в нижней части рис.5.5 (M = 50)
DIMENSION X(140),Y(140),A(100),B(100)
READ 1,Y
1 FORMAT(7F10.3)
X(1)=0.
DO 2 I=1,137
2 X(I+1)=X(I)+.1
CALL PAGE(17.,25.5,0,0,0)
CALL MINMAX(Y,137,YN,YX)
CALL LIMITS(0.,X(137),YN,YX)
CALL REGION(1.,.5,15.,7.5,0,0,0)
CALL LINEMO(X,Y,137,1,-1)
CALL FORIT(Y,68,50,A,B,IER)
CALL FORFIT(50,A,B,0.,X(137),150)
CALL ITALIC(1)
CALL SYMBOL(3.2,7.3,.5,'M=50',4,0)
CALL AXES(0,0,0.,5,0,0,200.,5,0)
CALL ENDPG('5.5')
END