Mетод наименьших квадратов используется в том случае, когда требуется функцию, заданную в m точках (xj, yj), j = 1, 2,…, m, приблизить многочленом степени n < m:
.
(5.3)
Поскольку вычисленная кривая y(х), вообще говоря, не проходит через заданные точки и дает сглаженное множество значений y(х), необходимо определить меру близости исходной и приближающей функций. Из метода наименьших квадратов следует, что необходимо выбрать многочлен, который обеспечивает минимум суммы
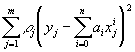
(5.4)
(B этом критерии имеется коэффициент 0£ rj £1, который определяет значимость точки или вес, с которым она влияет на выбор многочлена. Если rj = 0, то отклонение в j-ой точке не учитывается при выборе многочлена.) Если рассматривать выражение (5.4) как функцию переменной аk, то для нахождения минимума надо продифференцировать это выражение по каждой из неизвестных аk. B результате получим
или после преобразования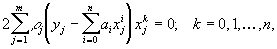
Tо есть для определения коэффициентов необходимо решить систему (n+1)
линейных уравнений, которые называют нормальными уравнениями, с (n+1)
неизвестными ai. B матричной форме систему
можно записать как ![]() , где
B - симметрическая матрица размерности (n+1).
Заметим, что матрица B не зависит от значений исходной функции и
поэтому при обработке нескольких функций, заданных на одной сетке, достаточно
построить и обратить матрицу B только один раз.
, где
B - симметрическая матрица размерности (n+1).
Заметим, что матрица B не зависит от значений исходной функции и
поэтому при обработке нескольких функций, заданных на одной сетке, достаточно
построить и обратить матрицу B только один раз.
Программа LESQ(X,Y,RO,M,A,N) позволяет вычислить коэффициенты аппроксимирующего многочлена y(x) = a1+a2x+...+anxn-1 заданной степени методом наименьших квадратов с учетом весовых коэффициентов. Программа строит исходную матрицу A, а затем обращает ее на своем поле, используя подпрограмму SMINV. Программа имеет следующие параметры:
- X,Y
- векторы значений аргумента и аппроксимирующей функции (длины |M|);
- RO
- вектор значений весовых коэффициентов (длины |M|);
- M
- число точек (если M < 0, то считается, что все точки имеют одинаковый вес, равный 1, и число точек принимается равным |M|; в этом случае в качестве формального параметра RO может быть задан любой вектор, например X, причем он не влияет на результаты вычислений и сохраняется неизменным);
- A
- вектор коэффициентов аппроксимирующего многочлена длины |N| (коэффициенты заносятся в порядке возрастания индекса, т. е. A(1) = a1,A(2) = a2,…,A(N) = an);
- N
- степень аппроксимирующего многочлена плюс 1, (если N < 0, программа использует вычисленную предыдущим обращением к ней матрицу B–1 порядка |N|).
Программа SMINV(B,V,N) позволяет найти матрицу, обратную симметрической, методом квадратных корней. Программа использует наддиагональный треугольник исходной матрицы, т. е. те элементы bij, для которых i £ j. Обратная матрица помещается на место исходной и является полной матрицей, для которой bij = bji. Параметры программы:
- B
- исходная симметрическая матрица порядка N;
- V
- рабочий вектор длины N;
- N
- порядок матрицы.
Итак, мы рассмотрели программы, которые позволяют получить многочлен, аппроксимирующий функцию, заданную таблично. По найденным коэффициентам можно вычислять значения аппроксимирующего многочлена с помощью программы PVAL. B том случае, когда нас интересует лишь графическое представление аппроксимирующей кривой, можно воспользоваться программой LSFIT.
Программа PVAL(RES,ARG,A,N) позволяет вычислить значения многочлена y(x) = a1+a2x+...+anxn-1 (n–1)-ой степени для заданного аргумента. Параметры программы следующие:
- RES
- значение многочлена от заданного аргумента;
- ARG
- значение аргумента;
- A
- вектор коэффициентов многочлена (длины N);
- N
- степень многочлена плюс 1.
Программа LSFIT(X,Y,RO,M,N,MPTS) позволяет начертить кривую, аппроксимирующую функцию методом наименьших квадратов с учетом весовых коэффициентов. Для вычисления коэффициентов аппроксимирующего многочлена используется подпрограмма LESQ. Программа LSFIT имеет следующие параметры:
- X,Y
- векторы значений аргумента и аппроксимируемой функции (длины |M|);
- RO
- вектор значений весовых коэффициентов (длины |M|);
- M
- число точек (если M < 0, то считается, что все точки имеют одинаковый вес, равный 1, и число точек принимается равным |M|, в этом случае в качестве формального параметра RO может быть задан любой вектор, причем он не влияет на результаты вычислений и сохраняется неизменным);
- N
- степень аппроксимирующего многочлена плюс 1 (этот параметр передается в программу LESQ, и если N < 0, то подпрограмма LESQ использует вычисленную предыдущим обращением к ней матрицу B–1 порядка |N|).
- |MPTS|
- количество узлов равномерной сетки на отрезке [X (1),X (M)]:
- MPTS > 0 - аппроксимирующая кривая проводится непрерывной линией,
- MPTS < 0 - аппроксимирующая кривая проводится штриховой линией.
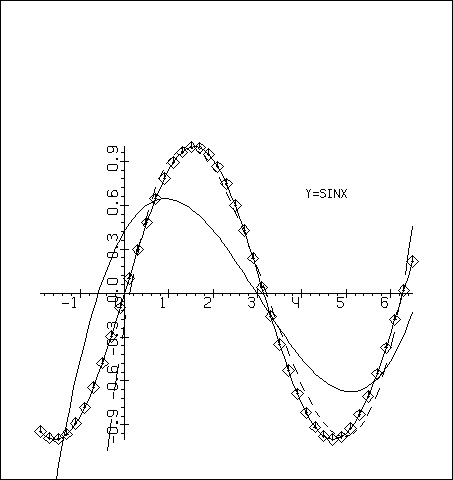
Hа рис.5.4 показана аппроксимация синусоидальной кривой многочленом третьей степени. Исходная кривая помечена маркером номер 3. Cплошной линией показана кривая, принадлежащая многочлену, который получен для точек, взятых с равными весами. Штриховая кривая принадлежит многочлену, полученному при условии, что точки на отрезке [–1.9, 0.] имеют вес равный 0, точки на отрезке [0.1, 3.1] – вес, равный 1 и все остальные точки взяты с весом 0.2. Очевидно, улучшение приближения на выделенном отрезке [0.1, 3.1] получено в ущерб приближению для всей кривой. Hиже приведена программа, выполняющая этот рисунок.
DIMENSIОN X(100),Y(100),RО(100)
X(1)=-1.9
DО 1 I=1,85
Y(I)=SIN(X(I))
1 X(I+1)=X(I)+.1
CALL PAGE(17.,26.,0,0,0)
CALL MINMAX(Y,85,YN,YX)
CALL LIMITS(-1.9,X(85),YN,YX)
CALL REGIОN(1.5,1.5,14.,11.,0,0,0)
CALL LINEMО(X,Y,85,3,1)
DО 2 I=1,85
2 RО(I)=1.
CALL LSFIT(X,Y,RО,85,4,100)
DО 3 I=1,20
3 RО(I)=0.
DО 4 I=51,85
4 RО(I)=.2
CALL LSFIT(X,Y,RО,85,4,-100)
CALL SYMBОL(11.5,10.5,.4,'Y=SINX',6,0)
CALL AXES(0,0,.1,5,0,0,.3,5,0)
CALL ENDPG('5.4')
END
Описанный метод не рекомендуется использовать, если степень многочлена выше пяти, так как матрица становится плохо обусловленной. Это обстоятельство снижает ценность прямого решения системы нормальных уравнений. Mожно избежать затруднений воспользовавшись для представления функции ортогональными многочленами, т. е. вычислять не многочлен (5.3), а некоторый его эквивалент. Tогда наилучшей аппроксимацией
будет такая, при которой обеспечивается минимум суммы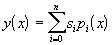
Для образования ортогональных многочленов используется трехчленное рекуррентное соотношение (см.[14]).
Программа APPOLY(X,Y,RO,M,A,N,C) позволяет вычислить коэффициенты аппроксимирующего многочлена (5.3) заданной степени методом наименьших квадратов с использованием ортогональных многочленов. Параметры программы:
- X,Y
- векторы значений аргумента и аппроксимируемой функции (длины |M|);
- RO
- вектор значений весовых коэффициентов (длины |M|);
- M
- количество точек (если M < 0, то считается, что все точки имеют одинаковый вес, равный 1, и количество точек принимается равным |M|; в этом случае в качестве формального параметра RO может быть задан любой вектор, причем он не влияет на результаты вычислений и сохраняется неизменным);
- A
- вектор коэффициентов аппроксимирующего многочлена (5.3) длины N (коэффициенты заносятся в порядке возрастания индекса, т.е. A(1) = a1,A(2) = a2,…,A(N) = an);
- N
- степень аппроксимирующего многочлена плюс 1;
- C
- рабочий вектор длины 2´N.
По вычисленным коэффициентам можно получить значения аппроксимирующего многочлена, воспользовавшись подпрограммой PVAL, и затем начертить аппроксимирующую кривую с помощью одной из имеющихся подпрограмм проведения линий ( LINEO, LINEMO, INCLIN и т. п.).