5.8.Аппроксимация методом Безье

В системах автоматизации проектирования и производства для конструирования кривых и поверхностей применяется аппроксимация методом Безье. Сущность метода заключается в следующем.

Пусть задана совокупность из (n+1) точек кото­рую будем называть ломаной Безье. Кривая Безье, соответствующая этой ломаной, описывается в виде функции параметра t следующим полиномом:

,
(5.11)
где - радиус-вектор точек на кривой, а Jni(t) - аппроксими­рующие многочлены Бернштейна, равные
.
(5.12)

Здесь 0 £t £1 и, кроме того, предполагается, что ti = 1 при i = 0 и t = 0.

Ломаная Безье однозначно определяет форму кривой Безье. Изменяя положения вершин ломаной, можно управлять формой соот­ветствующей кривой Безье. При этом следует иметь в виду следую­щее:

1. самой кривой в общем случае будут принадлежать только первая и последняя вер­ши­ны ло­ма­ной Безье, остальные вершины бу­дут лишь оказывать влияние на вид и гладкость кри­вой (рис.5.8);

2. наклоны касательных векторов в крайних точках кривой Безье и ломаной Безье сов­па­да­ют (рис.5.8), поэтому при со­пряжении двух кривых Безье, заданных ломаными и , одинаковый наклон кривых в точке соединения получа­ется в том случае, если точ­ки (которая совпадает с ) и лежат на одной прямой;

3. как видно из выражений (5.11) и (5.12), степень аппрокси­мирующего полинома рав­на n (т.е. числу звеньев в ломаной Безье), поэтому для увеличения порядка кривой Безье дос­та­точ­но лишь задать дополнительные вершины в соответствующей ломаной Безье;

4. кривая Безье всегда целиком лежит внутри выпуклой оболоч­ки ломаной Безье.

Метод аппроксимации Безье реализован в программах BEZ2 и BEZ3, с помощью которых можно построить соответственно двумерные и трехмерные кривые Безье.

Программа BEZ2(XP,YP,NPLG,XC,YC,NPTS) позволяет вычислить значения координат точек плоской кривой, аппроксимирующей задан­ную совокупность точек методом Безье. Программа имеет следующие параметры:

XP,YP
векторы значений соответственно X-, и Y-координат заданной со­во­куп­нос­ти точек (ломаной Безье) длины NPLG;
NPLG
число точек в ломаной Безье;
XC,YC
векторы значений соответственно X-, и Y-координат аппроксимирующей кривой Безье длины NPTS.
NPTS
число точек в аппроксимирующей кривой Безье.

Программа BEZ3(XP,YP,ZP,NPLG,XC,YC,ZC,NPTS) позволяет вычис­лить значения координат точек пространственной кривой, аппрокси­мирующей заданную совокупность точек методом Безье. Параметры программы следующие:

XP,YP,ZP
векторы значений соответственно X-, Y- и Z-ко­ординат заданной со­во­куп­нос­ти точек (ломаной Безье) длины NPLG;
XC,YC,ZC
векторы значений соответственно X-, Y- и Z-ко­ординат ап­прок­си­ми­рую­щей кривой Безье (длины NPTS).

Параметры NPLG и NPTS имеют то же значение, что и в про­грамме BEZ2.


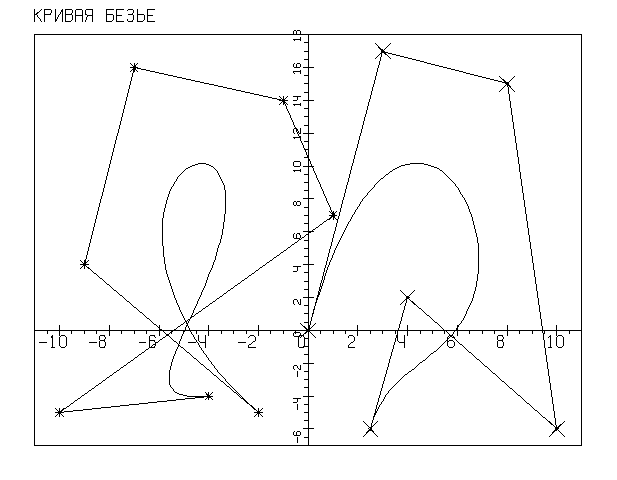
Рис.5.8. Пример аппроксимации методом Безье.

На рис.5.8 показаны ломаные Безье и соответствующие им кри­вые Безье. Построение выполнялось с помощью следующего фрагмента программы. 

     PARAMETER(NL=5,NS=41,NL1=4,NS1=61)
     REALXC(NS),YC(NS),XP(NL),YP(NL)
     REALXC1(NS1),YC1(NS1),XP1(NL1),YP1(NL1)
     DATAXP/0.,3.,10.,9.,4./,YP/0.,13.,17.,-6.,2./
     DATAXP1/-2.,-9.,1.,-10./,YP1/-5.,7.,7.,-5./
     CALL GRINIT
     CALL BEZ2(XP,YP,NL,XC,YC,NS)
     CALL BEZ2(XP1,YP1,NL1,XC1,YC1,NS1)
     CALL PAGE(18.,14.,'5.8',3,0)
     CALL REGION(1.,1.,16.,12.,'КРИВАЯ БЕЗЬЕ',12,1)
     CALL LIMITS(-11.,11.,-7.,18.)
     CALL AXES('X',1,0.,4,'Y',1,0.,4,0)
     CALL LINEMO(XP,YP,NL,2,1)
     CALL LINEO(XC,YC,NS)
     CALL LINEMO(XP1,YP1,NL1,-7,1)
     CALL LINEO(XC1,YC1,NS1)
     CALL ENDPG(0)
     END

Для изображения пространственных кривых Безье можно восполь­зоваться прог­рам­ма­ми, описанными в п.8.1.3. При этом могут ока­заться полезными также средства по­вы­ше­ния наглядности изображе­ния (см. п.8.4.4, рис.8.33).