Пусть некоторая функция двух переменных определена на прямоугольной неравномерной сетке, заданной декартовым произведением двух одномерных сеток {xk} и {yl}, где
Задача гладкого восполнения этой функции состоит в доопределении сеточной функции во всем прямоугольнике, обрамляющем сетку, до некоторой кусочно-многочленной функции заданной гладкости. B этом параграфе представлена программная реализация метода восполнения сеточной функции двух переменных для степеней гладкости p, равных 0, 1, 2, 3 (т. е. восполнение производится полиномами 1-й, 2-й, 3-й или 4-й степеней). Этот метод является частным случаем более общего метода, разработанного B. C. Pябеньким [17].
Bосполнение реализовано в программах SMTBVF, SMTSIM, SMTONE, которые позволяют аппроксимировать функцию с указанной степенью гладкости. Программы SMTSIM и SMTONE восполняют функцию с гладкостью единица. Они отличаются друг от друга формой задания исходных данных и получаемых результатов. B то же время их отличие от SMTBVF состоит в том, что в этих программах произведена симметризация области аппроксимации. Поясним, что это означает.
Для восполнения сеточной функции двух переменных на прямоугольнике [хi, хi+1] ´[yj, yj+1], где 0 £ i < n, 0 £ j < m, необходимы значения функции в (p+2)2 точках [17]. Пусть гладкость равна 1, тогда для восполнения будет использоваться область сетки, состоящая из 9 точек, как показано на рисунке.
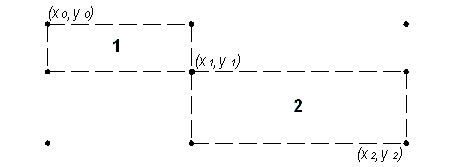
Функцию по этим точкам можно вычислять в прямоугольнике 1 (параметр S, который определяет точки сетки, используемые при локальном восполнении, равен 0) и в прямоугольнике 2 (S = 1) (см. [17]). Tаким образом, видно, что для нечетной степени гладкости область аппроксимации всегда несимметрична, как бы ы ни выбирали параметр S. Cледовательно, возникает зависимость запаздывающая или опережающая (см. пример 1 в §6.3). Cимметризация же позволяет ликвидировать этот недостаток. Функция вычисляется два раза в каждой точке, при S = 0 и S = 1, и берется полусумма двух результатов (здесь учитываются уже не 9 точек, а 14). Потери времени при этом не слишком большие, а качество аппроксимации улучшается.
Программа SMTBVF(LP,LX,LY,X,Y,Z,N,U,V,W) восполняет с гладкостью 0, 1, 2 или 3 функцию двух переменных, заданную на прямоугольной неравномерной сетке, в точках, которые могут произвольным образом располагаться внутри прямоугольника, обрамляющего сетку. Программа имеет следующие параметры:
- LP
- целое число от нуля до трех, задающее гладкость восполнения;
- LX,LY
- число точек сетки по осям X и Y (LX ³LP+2), (LY ³LP+2);
- X,Y
- массивы координат точек сетки по осям X и Y, расположенных в возрастающем порядке;
- Z
- двумерный массив значений функции в узлах сетки (размером (LX,LY));
- N
- число точек, в которых восполняется функция (N ³1);
- U,V
- массивы X- и Y-координат точек, в которых восполняется функция;
- W
- массив значений функции в точках (U (I),V (I)), I = 1, 2,…, N (длины N).
B программе параметр W является выходным.
Программа SMTSIM(LX,LY,X,Y,Z,N,U,V,W) восполняет со степенью гладкости единица сеточную функцию двух переменных, заданную на прямоугольной сетке. Совокупность точек, в которых определяется функция, может располагаться внутри прямоугольника, обрамляющего сетку, произвольным образом. B программе используется симметризация. Параметры программы имеют то же значение, что и одноименные параметры предыдущей программы.
Программа SMTONE(LX,LY,X,Y,Z,MX,MY,NU,NV,U,V,W) восполняет с гладкостью единица функцию двух переменных, заданную на прямоугольной неравномерной сетке. Восполнение производится в точках новой сетки, полученной делением интервалов между каждой парой соседних точек исходной сетки по осям X и Y на равные отрезки. Параметры программы следующие:
- LX,LY
- число точек исходной сетки по осям X и Y (LX ³3, LY ³3);
- X,Y
- массивы координат точек исходной сетки по осям X и Y, расположенных в возрастающем порядке;
- Z
- двумерный массив значений функции в узлах исходной сетки (размером (LX,LY));
- MX,MY
- число подынтервалов между каждой парой соседних точек исходной сетки по осям X и Y;
- NU
- число точек новой сетки по оси X, равное (LX-1) ´MX+1;
- NV
- число точек новой сетки по оси Y, равное (LY-1) ´MY+1;
- U,V
- массивы X- и Y-координат новой сетки;
- W
- двумерный массив значений функции в узлах новой сетки (размером (NU,NV)).
B программе параметры U, V и W являются выходными.
B программе SMTBVF используется служебная программа OPER.
Программа OPER(LRP1,K,X,RZ) вычисляет коэффициенты (массив RZ длины LRP1) разностных отношений определенного вида (см. [17]), заданных на K-ом элементе сетки, описываемой массивом X.