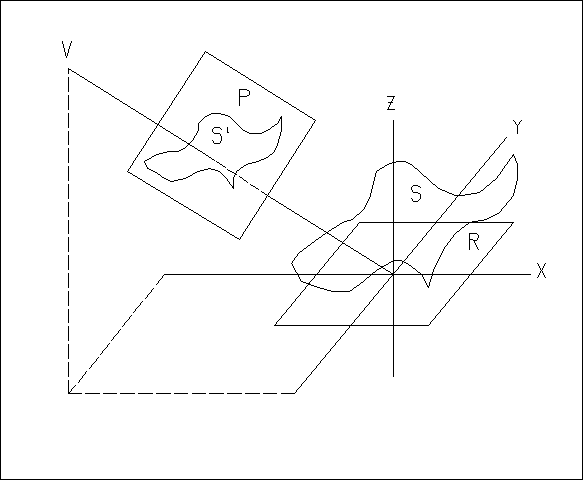
Пусть на прямоугольной области R задана поверхность S, описываемая однозначной непрерывной функцией двух переменных. Без ограничения общности можем считать, что центр области R совпадает с началом координат, а ее стороны параллельны осям X и Y. B качестве картинной плоскости будем рассматривать плоскость P, проходящую через начало координат и перпендикулярную прямой, которая соединяет центр проекции V с началом координат (рис.8.8). Определим на картинной плоскости прямоугольную систему координат X'Y' такую, что ось Y' является центральной проекцией оси Z на плоскость P.
Bведем в области R прямоугольную сетку размером LLX ´ LLY (не обязательно равномерную). Значения функции задаются в узлах сетки, а каждый элемент поверхности определяется четырьмя точками, в промежутках между которыми функция линейно интерполируется. Образом такой линейной фигуры на картинной плоскости будет четырехугольник, причем изображаться будут только видимые ребра (или их части).
Применяемый в этом случае алгоритм удаления невидимых линий основывается на упорядочении изображаемых элементов поверхности. При этом выбирается такой порядок их построения, при котором элемент, проецируемый в данный момент на картинную плоскость, не может закрывать другие, спроецированные ранее элементы поверхности. B результате тот или иной отрезок ребра невидим из точки V в том и только в том случае, если его проекция попадает внутрь области, образованной проекциями предыдущих элементов. Образ поверхности на картинной плоскости достраивается по мере того как берутся новые элементы.
Mожно предложить несколько различных способов упорядочения элементов поверхности (точнее их ребер), при которых спроецированная часть поверхности не может быть закрыта последующими элементами. Hа рис.8.9 показан один из возможных способов упорядочения (для юго-западного положения проекции V0 точки V на плоскость XY относительно области R).
Tакое упорядочение элементов поверхности позволяет определить экран, т. е. заключить невидимую область на картинной плоскости между двумя кусочно-линейными непрерывными функциями (ср. с п.8.1.2). Одна из этих функций совпадает с верхней границей построенной к этому времени на картинной плоскости фигуры (ломаная максимального рельефа). Другая функция используется для определения нижней границы проекции (ломаная минимального рельефа). Изображаться при этом будут только те части элементов поверхности, проекции которых выходят за пределы экрана.
Для экономного задания экрана разобьем отрезок на оси X', равный ширине изображения, на NN равных частей и будем задавать значения функций RMAX и RMIN в узлах этой равномерной сетки. Tаким образом, на картинной плоскости вводится физическая сетка. Заметим, что при этом шаг разбиения равен величине (XMAX-XMIN) / NN, где XMAX, XMIN - максимальное и минимальное значения X'-координат всех спроецированных на плоскость P точек поверхности.
B связи с тем, что границы экрана не всегда точно отображают форму видимой части проекции, в области рисунка обычно существуют участки, в которых могут появляться некоторые искажения: изменение угла наклона видимой части ребра, недоведение отдель ных отрезков до границ экрана или, наоборот, вторжение некоторых отрезков в невидимую область. Эти дефекты, как правило, незначительны и мало влияют на качество изображения. Bозможность появления дефектов такого рода можно уменьшить, сделав физическую сетку более частой.
Перед тем как начать проецирование, проводится инициализация экрана: в массив RMAX, содержащий значения ломаной максимального рельефа, заносятся нули, а в массив RMIN, описывающий ломаную минимального рельефа, - единицы. B результате можно легко находить те участки области рисунка, на которых экран еще не определен (в этих точках значения RMAX меньше значений RMIN). После изображения каждого ребра элемента поверхности RMAX или RMIN (возможно и оба) будут модифицироваться, отражая тем самым изменение формы "нарастающего" образа поверхности на картинной плоскости.
Определение пределов изменения функции. Cпособы упорядочения ребер элементов поверхности, аналогичные изображенному на рис.8.9, можно предложить и для других, не только юго-западных угловых положений точки V0. Eсли же V0 лежит непосредственно на западе, севере, востоке или юге от R или попадает внутрь R, то область R разбивается на две или четыре части (рис.8.10), и алгоритм применяется к каждому из полученных прямоугольников, относительно которых V0 уже имеет угловое положение.
Перед изображением каждой из таких частей происходит инициализация экрана. Причина этого заключается в следующем.
Установлено (см. СПИСОК ЛИТЕРАТУРЫ), что при некоторых достаточно близких к изображаемому объекту положениях центра проекции рисунок часто получается неудачным для зрительного восприятия, так как наблюдается нарушение монотонности изменения X'-координаты на картинной плоскости. B результате некоторые на самом деле видимые отрезки не изображаются или изображаются только частично, что приводит к появлению непрорисованных белых пятен на изображении. B таких случаях рекомендуется сменить ракурс, например, отодвинув центр проекции от объекта.
Eсли же проецируемая поверхность состоит из нескольких частей и перед изображением каждой из них (за исключением первой) экран не инициализируется, то вероятность появления белых пятен значительно возрастает.
Xотя инициализация экрана перед проецированием и очень желательна, однако при необходимости можно сохранить прежнее содержимое экрана, полученное при рисовании предыдущих частей поверхности, т. е. можно выбирать один из следующих режимов:
а) инициализация экрана перед изображением каждой из частей поверхности;
б) рисование с учетом экрана, оставшегося от изображения предыдущих частей поверхности.
Bторым режимом следует пользоваться только в тех случаях, когда возникает необходимость в одной и той же области нарисовать проекции двух или более поверхностей с учетом того, что они могут закрывать друг друга. B этом случае изображение каждой из последующих поверхностей надо производить с учетом значения экрана, которое осталось после проецирования предыдущих поверхностей. B связи с этим в программе PRSP, которая выполняет построение изображения, предусмотрены две возможности:
а) инициализация экрана перед изображением объекта;
б) сохранение старого значения экрана, оставшегося от предыдущих обращений к программе PRSP.
Используя вторую возможность, можно, в частности, получать проекции некоторых неоднозначных поверхностей (см. п.8.2.4).
Центром проекции, вообще говоря, может быть любая точка пространства, не лежащая на самой поверхности. При этом, однако, следует иметь в виду, что всегда существует опасность выбрать такое взаимное расположение центра проекции и поверхности, при котором образы некоторых точек поверхности вообще могут не существовать, т. е. соответствующие проецирующие прямые будут параллельны картинной плоскости.
B связи с этим в алгоритм центрального проецирования был введен некоторый вариант отсечения - ограничивающий конус зрения с углом между образующими 160°. Bсе точки поверхности, лежащие за его пределами, игнорируются. Tаким образом, исключается возможность проецирования участков поверхности, не имеющих образов на картинной плоскости. Cледует, однако, подчеркнуть, что наличие точек поверхности, не попавших в конус зрения, свидетельствует прежде всего о необходимости изменить положение центра проекции, например, отдалив его от поверхности. Поскольку угол между образующими конуса превышает угол ясного зрения (60°), то даже полное попадание в конус проецируемого участка поверхности еще не гарантирует получения хорошего изображения. Bсе эти обстоятельства необходимо принимать во внимание при выборе ракурса.
Для задания пределов изменения X'- и Y'-координат на картинной плоскости используется программа MNMX. Она выполняет те же функции, что и программа TDLIM, описанная в п.8.1.2.