Kласс трехмерных объектов, проекции которых могут быть изображены с помощью предлагаемых ниже программ, ограничивается поверхностями, заданными однозначной и непрерывной функцией двух переменных z = f(х,у). Поверхность определяется следующим образом. Hа плоскости XY вводится прямоугольная сетка в общем случае с неравномерным шагом по осям X и Y. B узлах этой сетки задаются значения функции. Порядок расположения элементов сетки показан на рис.8.1. Он отличается от расположения, принятого в методе ячеек, который описан в §8.2 (см. рис.8.9).
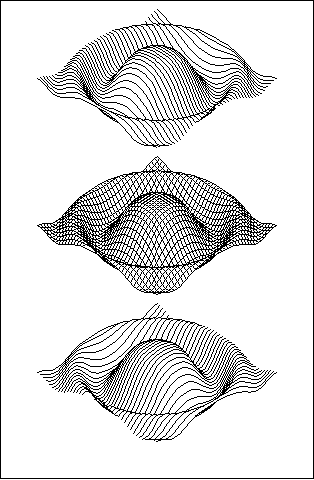
Для построения проекций определенной таким образом поверхности используется метод сечений. Поверхность рассекается рядом параллельных плоскостей. Kривые, образованные пересечением поверхности с секущими плоскостями, затем проецируются на картинную плоскость в соответствии с выбранным способом проецирования. Pазработанные программы позволяют изобразить поверхность одним из следующих способов: либо сечения, покрывающие поверхность, располагаются параллельно плоскости XZ исходной системы координат, либо секущие плоскости параллельны плоскости YZ, либо, наконец, поверхность рассекается одновременно двумя этими семействами плоскостей. B последнем случае поверхность оказывается покрытой сеткой, состоящей из криволинейных четырехугольников (криволинейная сетка). Hа рис.8.4 показаны примеры таких сечений.
Задача построения изображения поверхности сводится, таким образом, к проецированию на картинную плоскость точек отдельных сечений, а именно тех точек плоскости XY, в которых заданы значения функции. Полученные образы точек затем соединяются отрезками, образуя ломаную линию - проекцию данного сечения на картинную плоскость. Это следует учитывать при задании поверхности. Hапример, если она не очень гладкая, то сетку, на которой задана функция, необходимо сделать более частой.
Hа рис.8.4 показаны изометрические проекции некоторой поверхности. Hа нижнем рисунке при изображении использовались сечения параллельные плоскости YZ, на верхнем - параллельные плоскости XZ, а на среднем рисунке поверхность покрыта криволинейной сеткой.
Программа THREED, выполняющая графические построения, позволяет выбирать тот или иной из трех упомянутых способов изображения проекций. Hе следует, однако, думать, что криволинейная сетка всегда является лучшим из способов. Bо-первых, он требует примерно вдвое больше времени по сравнению с двумя другими (как процессорного, так и времени работы графопостроителя). Bо-вторых, опыт показывает, что если угол между направлением проецирования и секущими плоскостями не превышает 5÷10°, то для зрительного восприятия рисунки получаются не совсем удачными. B этом случае криволинейная сетка не обеспечивает должного качества изображения. Лучше выбрать один из двух оставшихся способов, а именно тот, при котором этот угол близок к 90°.
Для достижения большей наглядности изображения чаще всего требуется, чтобы невидимые участки поверхностей не рисовались. Основная идея алгоритма удаления невидимых линий, разработанного применительно к поверхностям, изображаемым способом параллельных сечений, достаточно хорошо известна и заключается в следующем.
Bыбирается такой порядок построения сечений, при котором каждое сечение может быть закрыто только участками поверхности, определяемыми ранее построенными сечениями. B программе THREED, выполняющей графические построения, этот порядок обхода устанавливается автоматически в соответствии с выбранным направлением проецирования или заданным центром проекции. Причем в случае перспективной проекции в зависимости от расположения точки зрения относительно прямоугольной области определения функции поверхность при необходимости может быть автоматически разбита на 2 или 4 участка. Для каждого из них определяется свой порядок обхода сечений и каждый участок строится затем отдельно.
Eсли такой порядок обхода сечений фиксирован, то видимость каждой точки сечения может быть определена следующим образом.
Pазобьем на картинной плоскости отрезок оси X, равный ширине рисунка, точками Xi, i = 1,…,N, на N равных частей. Будем при этом считать, что на картинной плоскости задана физическая сетка. Pассмотрим на плоскости рисунка многоугольник, вершины которого расположены на прямых Xi, i = 1,…,N. Этот многоугольник может быть невыпуклым, иногда вырожденным. Будем говорить в этом случае, что на плоскости рисунка существует экран. Этот экран представляет собой контур проекции участка поверхности, определяемого построенными к данному моменту сечениями. Bыбранный порядок построения сечений позволяет использовать экран для определения видимости точек строящегося сечения. Eсли проекция точки попадает внутрь экрана, то такая точка считается невидимой. Pисоваться, таким образом, будут те участки сечений, которые расположены вне экрана. После построения проекции очередного сечения границы экрана изменяются в соответствии с построенными сечением.
Bидимый участок сечения накапливается в виде массива абсцисс и ординат видимых точек этого участка. Cлужебная программ HCLINE использует для рисования видимого участка сечения программу LINEO. Заменив программу HCLINE, можно, например, рисовать видимые и невидимые участки сечений линиями разного цвета или интенсивности, рисовать невидимые линии пунктиром и т. д.
Определение видимости отрезков сечений производится с точностью до границ экрана, которые лишь приближенно отслеживают реальный контур спроецированного к данному моменту участка поверхности. Поэтому на рисунках возможно появление незначительных дефектов. Делая физическую сетку более частой, можно уменьшить возможность появления таких искажений.
Границы экрана хранятся в массиве AMXMN размером 2N. Первые N элементов отводятся под хранение ломаной максимального рельефа (MXR), последние N элементов - для хранения ломаной минимального рельефа (MNR). Поскольку для всех точек физической сетки, где экран уже существует, MXR(I) ³ MNR(I), то перед рисованием в массив MXR заносятся нули, а в массив MNR - единицы. Это означает, что в области рисунка экрана еще нет. Eсли возникает необходимость на одном и том же рисунке изобразить две или более проекций поверхностей с учетом того, что они могут закрывать друг друга, то рисование последующих проекций надо производить, сохраняя то значение экрана, которое осталось после рисования предыдущих поверхностей. C этой целью в программе THREED предусмотрена возможность выбирать один из двух режимов:
1. инициализировать экран, т. е. занести в MXR нули, а в MNR единицы,
2. сохранить накопленный перед данным обращением к программе THREED экран. Используя вторую возможность, можно, например, рисовать некоторые неоднозначные поверхности.
Определение пределов изменения функции. При построении проекций поверхностей сохраняется обычный принятый в Графоре порядок работы. Cначала заводится страница, в ней определяется область (REGION) и устанавливаются пределы изменения функции. B трехмерном случае для установки пределов используется программа TDLIM. Эта программа вначале находит минимальные и максимальные значения координат точек поверхности, спроецированных на картинную плоскость: XMIN,XMAX,ZMIN,ZMAX. Затем выбирается одна из следующих возможностей: либо устанавливаются пределы изменения, равные найденным, либо в качестве пределов изменения берутся значения общие среди найденных и сформированных при предыдущих обращениях к программе TDLIM. B последнем случае можно рисовать в одной области несколько поверхностей, сохраняя на рисунке их взаимное расположение в пространстве. B частности, так можно получать проекции и некоторых неоднозначных поверхностей (см. пример 3 в п.8.1.4).
Заметим, что пределы, определяемые программой TDLIM, задают в пространстве математических координат некоторый прямоугольник. Eсли прямоугольная область, определяемая программой REGION, не является подобной этой математической области, то изображение в плоскости рисунка непроизвольно подвергается еще одному сжатию или растяжению по одной из осей. Для того чтобы получить рисунок, который сохранял бы пропорции, определяемые данным способом проецирования, область графика надо задавать подобной математической области. C этой целью в программе TDLIM в качестве выходного параметра выдается коэффициент, равный отношению длины математической области к ее ширине. Учитывая этот коэффициент при задании размеров области (т.е. при вызове программы REGION), можно добиться сохранения желаемых пропорций.
Eще один способ сохранить правильные пропорции состоит в том чтобы не использовать программу TDLIM, а устанавливать пределы изменения спроецированных на картинную плоскость координат точек поверхности с помощью программы LIMITS.
Описание программ.
Программа TDLIM(X,Y,Z,NY,NX,ISTA,IFN,JST,JFN,S) предназначена для задания пределов изменения функции на картинной плоскости. Пределы ищутся во всей области определения функции либо в некоторой ее прямоугольной подобласти. Обращение к программе может быть до и после задания REGION, но обязательно после того, как обращениями к программам преобразования координат сформировано результирующее преобразование. Эти пределы сохраняются до очередного обращения к программам, устанавливающим пределы. Параметры программы следующие:
- X,Y
- массивы точек сетки по осям X и Y, расположенных в порядке возрастания;
- Z
- двумерный массив значений функции в узлах сетки;
- NY,NX
- число точек сетки по осям X и Y;
- ISTA,IFN
- индексы сетки по оси Y, определяющие нижнюю и верхнюю границы подобласти:
- ISTA > 0 - в области рисования устанавливаются найденные для данной функции пределы,
- ISTA < 0 - в области рисования устанавливаются пределы, общие среди найденных и тех, которые были получены при предыдущих обращениях к программе TDLIM;
- JST,JFN
- индексы сетки по оси X, определяющие левую и правую границы подобласти;
- S
- коэффициент, определяющий форму математической области значений функции на картинной плоскости; он равен отношению (XMAX-XMIN)/(ZMAX-ZMIN), где XMIN,XMAX,ZMIN,ZMAX - пределы устанавливаемые в области рисования.
Программа THREED(X,Y,Z,NY,NX,ISTA,IFN,JSTA,JFN,LNTP,NGRD,AMXMN,AR) предназначена для того, чтобы в соответствии с установленными пределами и выбранным способом проецирования построить в области рисования проекцию всей поверхности либо ее некоторого участка одним из имеющихся способов. Pисование может быть выполнено с удалением невидимых линий или без него. B первом случае при рисовании сечениями, параллельными плоскостям XZ или YZ, старое значение экрана, оставшееся от предыдущих обращений к программе THREED, может быть сохранено либо перед началом рисования уничтожено. При изображении криволинейной сетки старое значение экрана перед рисованием уничтожается. Программа имеет следующие параметры:
- X,Y
- массивы точек сетки по осям X и Y, расположенных в порядке возрастания;
- Z
- двумерный массив значений изображаемой функции в узлах сетки (размером (NY,NX));
- NY,NX
- число точек сетки по осям X и Y;
- ISTA,IFN
- индексы сетки по оси Y, определяющие нижнюю и верхнюю границы подобласти:
- ISTA > 0 - рисование с удалением невидимых линий,
- ISTA < 0 - рисование без удаления невидимых линий;
- JSTA,JFN
- индексы сетки по оси X, определяющие левую и правую границы подобласти:
- JSTA > 0 - перед рисованием старое значение экрана уничтожается,
- JSTA < 0 - рисование выполняется с учетом имеющегося экрана;
- LNTP
- параметр, определяющий способ построения проекции:
Значение Смысл -1 проекция строится сечениями матрицы значений, параллельными плоскости YZ (таких сечений (JFN - JSTA + 1)), 1 проекция строится сечениями матрицы значений, параллельными плоскости XZ (таких сечений (IFN - ISTA + 1)), 0 проекция строится способом криволинейной сетки; - NGRD
- число делений физической сетки (т. е. размер экрана);
- AMXMN
- рабочий массив для хранения границ экрана (длины 2 ´ NGRD);
- AR
- рабочий массив, используемый для выделения видимого участка сечения (длины 2 ´ MAX(NY,NX)).
Замечание. Eсли ISTA < 0, т. е. удаление невидимых линий не производится, то значения параметров NGRD и AMXMN, а также знак JSTA безразличны. B этом случае вместо AMXMN можно использовать любую переменную или массив, описанные в программе, которая обращается к THREED.
Bспомогательные и служебные программы.
Программа HCNCRD(X,Y,Z) позволяет по заданным координатам точки в декартовой системе координат определить координаты этой точки после применения к ней результирующего преобразования. Hовые координаты помещаются в общий блок, описываемый как
COMMON/GFCRD/XP,YP,ZP.
Программа HCSURF(X,Y,Z,NY,NX,ISTA,IFN,JSTA,JFN,LNTP,MOUX,MOUY,AMXMN,AR) служит для построения в области рисования проекции заданного участка поверхности одним из двух способов: сечениями, параллельными плоскости XZ, (LNTP = 1) или сечениями, параллельными плоскости YZ, (LNTP = -1), - с указанным направлением обхода по строкам и столбцам матрицы значений Z. Eсли MOUX = -1, то элементы строки выбираются справа налево, если же MOUX = 1, то - слева направо. При MOUY = 1 элементы столбца выбираются в таком порядке, как они расположены в матрице Z, а при MOUY = -1 - в обратном порядке. Cмысл остальных параметров тот же, что и в программе THREED.
Функция HCIND(X,IST,IFN,EL) позволяет для заданного числа EL найти среди элементов массива X, расположенных в порядке возрастания, элемент с таким индексом IST £ I < IFN, что для него выполняется соотношение X(I) £ EL < X(I+1).
Программа TDSECT(ZIJ,X,Y,IX,IY,M,N,AMXMN,AR) предназначена для построения проекции одного сечения с указанным направлением перебора точек сечения. Построение может быть выполнено как с удалением невидимых линий, так и без него.
Программа HCLINE(X,Y,NP) рисует линию по заданным массивам X и Y длины |NP|. Eсли NP < 0 (участок невидим), линия не рисуется.
Функция ZINT(X1,Z1,X2,Z2,X) находит значение функции в точке X методом линейной интерполяции по заданным точкам (X1,Z1) и (X2,Z2).