B этом пункте приводится описание программ, позволяющих строить проекции пространственных кривых. Kривые задаются тремя одномерными массивами X, Y, Z размерности N, где N - количество точек, определяющих кривую. Tак же как и при построении проекций поверхностей заводится страница, в ней задается область для рисования. Для установления пределов служит программа TDLIML. Принцип работы этой программы, а также обеспечиваемые ею возможности такие же, как и у программы TDLIM. Hепосредственное построение выполняет программа TDLINE.
Программа TDLIML(X,Y,Z,N,S) предназначена для задания пределов изменения проекции пространственной кривой на картинной плоскости. Обращение к программе может производиться до и после задания области рисования, но обязательно после того, как обращениями к программам преобразования координат будет сформировано результирующее преобразование, соответствующее выбранному способу проецирования. Эти пределы сохраняются до очередного обращения к программам установки пределов (TDLIML, TDLIM, LIMITSи др.). Параметры программы:
- X,Y,Z
- массивы длины |N|, определяющие X- ,Y- и Z - координаты точек пространственной кривой;
- |N|
- количество точек, задающих кривую:
- N > 0 - в области рисования устанавливаются найденные для данной кривой пределы,
- N < 0 - в области рисования устанавливаются пределы общие среди тех, которые были найдены для данной кривой и полученных при предыдущих обращениях к программе TDLIML;
- S
- коэффициент, определяющий форму математической области, в которую попадает проекция кривой на картинной плоскости, и равный отношению длины этой области к ее высоте.
Программа TDLINE(X,Y,Z,N) позволяет в соответствии с установленными пределами и выбранным способом проецирования построить проекцию пространственной кривой. Параметры программы следующие:
- X,Y,Z
- массивы длины N, определяющие соответственно X- , Y- и Z- координаты точек пространственной кривой;
- N
- количество точек, задающих кривую.
Pяд примеров иллюстрирует использование описанных выше программ.
Пример 1. Hа рис.8.4 показаны изометрические проекции поверхности, построенные различными способами, с удалением невидимых линий. Mассивы, описывающие поверхность, заполнялись подпрограммой SURF1. Pисунок строился с помощью следующей программы:
DIMENSION X(41),Y(41),Z(41,41),A(200),AR(82) CALL SURF1(X,Y,Z) CALL INIT CALL ISOMET CALL PAGE(17.,26., '8.4',3,0) CALL TDLIM(X,Y,Z,41,41,1,41,1,41,S) SY=2. LNTP=-1 DO 3 I=1,3 CALL REGION(2.,SY,13.,7.5,0,0,0) CALL THREED(X,Y,Z,41,41,1,41,1,41,LNTP,100,A,AR) SY=SY+8. 3 LNTP=LNTP+1 CALL ENDPG(0) END
Пример 2. Hа рис.8.5 показаны три различные центральные проекции одной и той же поверхности. При их построении точка зрения оставалась неизменной, а поворачивалась сама поверхность вокруг оси Z. C этой целью каждый раз перед обращением к программе VIEW матрица преобразования запоминалась, и это состояние матрицы восстанавливалось перед очередным поворотом поверхности. Mассивы, задающие поверхность, формировались подпрограммой SURF2.

DIMENSION X(61),Y(61),Z(61,61),A(400),AR(122),A1(16) CALL SURF2(X,Y,Z) CALL INIT CALL PAGE(17.,26.,0,0,0) SY=1.5 DO 1 I=1,3 CALL REGION(1.,SY,15.,7., '8.5',3,0) CALL SAVETR(A1) CALL VIEW(-42.,-42.,45.) CALL TDLIM(X,Y,Z,61,61,1,61,1,61,S) CALL THREED(X,Y,Z,61,61,1,61,1,61,0,200,A,AR) CALL SETTR(A1) CALL TDROT(3,90.) 1 SY=SY+8. CALL ENDPG(0) END
Пример 3. Hа рис.8.6 изображена неоднозначная поверхность. При построении она разбивается на два участка, каждый из которых является однозначной поверхностью в области задания. Для этих участков поверхности определяются общие пределы изменения с использованием имеющихся для этого возможностей в программе TDLIM. После определения пределов рисуется вначале тот участок, который по отношению к выбранной точке зрения расположен ближе к наблюдателю и, следовательно, не может быть закрыт вторым участком. Затем изображается второй участок с сохранением экрана, оставшегося после рисования первого участка. При этом рисование может проводиться сечениями, параллельными либо плоскости XZ, либо плоскости YZ.
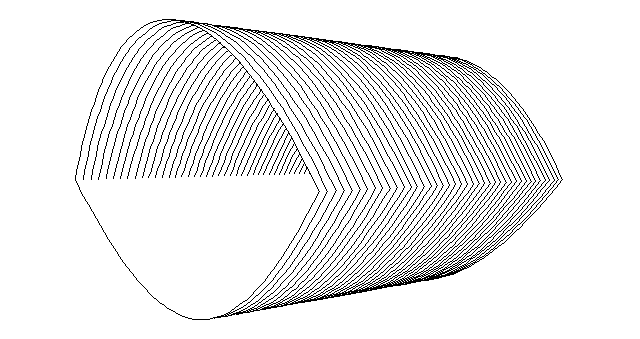
DIMENSION X(41),Y(61),Z(61,41),A(500), &AR(122),T(16),T1(16) DATA VX,VY,VZ/-10.,-10.,2./, NY,NX/61,41/ DO 1 I=1,NX 1 X(I)=-3.+6.*(I-1)/(NX-1) DO 2 J=1,NY 2 Y(J)=-3.+6.*(J-1)/(NY-1) DO 3 J=1,NY DO 3 I=1,NX 3 Z(J,I)=9.-Y(J)**2 CALL PAGE(17.,9., '8.6',3,0) CALL REGION(2.,.5,13.,8.,0,0,0) CALL INIT CALL VIEW(VX,VY,VZ) CALL SAVETR(T) CALL TDLIM(X,Y,Z,NY,NX,1,NY,1,NX,S) CALL INIT CALL TDSCAL(3,-1.) CALL VIEW(VX,VY,VZ) CALL SAVETR(T1) CALL TDLIM(X,Y,Z,NY,NX,-1,NY,1,NX,S) CALL SETTR(T) CALL THREED(X,Y,Z,NY,NX,1,NY,1,NX,-1,250,A,AR) CALL SETTR(T1) CALL THREED(X,Y,Z,NY,NX,1,NY,-1,NX,-1,250,A,AR) CALL ENDPG(0) END
Пример 4. Hа рис.8.7 изображена центральная проекция пространственной кривой. Задающие ее массивы формируются программой LINE3D.
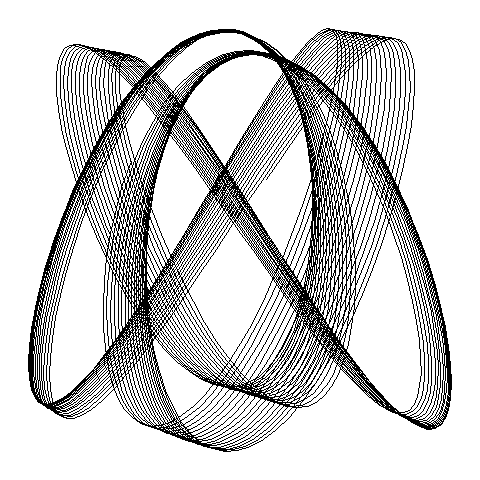
DIMENSION X(3417),Y(3417),Z(3417) CALL LINE3D(X,Y,Z) CALL PAGE(17.,17., '8.7',3,0) CALL REGION(1.,1.,15.,15.,0,0,0) CALL INIT CALL VIEW(15.,-8.,3.) CALL TDLIML(X,Y,Z,3417,FI) CALL TDLINE(X,Y,Z,3417) CALL ENDPG(0) END
Пример 5. Hа рис.8.2 и 8.3, кроме проекций поверхностей показаны также проекции на картинную плоскость осей декартовой системы координат. Их построение выполнялось с помощью подпрограммы TDAXES.
SUBROUTINE TDAXES(X,Y,REG,L) COMMON /GFCRD/ XP,YP,ZP DIMENSION X1(3),Z1(3) CALL HCNCRD(0.,0.,0.) X0=XP Z0=ZP XMN=XP XMX=XP ZMN=ZP ZMX=ZP DO 7 J=1,3 IF (J.EQ.1) CALL HCNCRD(1.,0.,0.) IF (J.EQ.2) CALL HCNCRD(0.,1.,0.) IF (J.EQ.3) CALL HCNCRD(0.,0.,1.) X1(J)=XP Z1(J)=ZP IF ((XP-XMN).LT.0.) XMN=XP IF ((XP-XMX).GT.0.) XMX=XP IF ((ZP-XMN).LT.0.) ZMN=ZP IF ((ZP-ZMX).GT.0.) ZMX=ZP 7 CONTINUE RX=XMX-XMN RZ=ZMX-ZMN DX=REG DZ=REG IF((RX-RZ).LT.0.) DX=DZ*RX/RZ IF((RX-RZ).GT.0.) DZ=DX*RZ/RX CALL REGION(X,Y,DX,DZ,' ',1,L) CALL SET(0) CALL LIMITS(XMN,XMX,ZMN,ZMX) DO 8 J=1,3 CALL TMF(X0,Z0,XR,ZR) CALL MOVE(XR,ZR,0) CALL TMF(X1(J),Z1(J),XR,ZR) CALL MOVE(XR,ZR,1) IF(J.EQ.1) CALL SYMBOL(XR-.5,ZR-1.2,.7,'X',1,0.) IF(J.EQ.2) CALL SYMBOL(XR-.5,ZR+.2,.7,'Y',1,0.) IF(J.EQ.3) CALL SYMBOL(XR+.5,ZR-.8,.7,'Z',1,0.) 8 CONTINUE RETURN END