8.1.1. Преобразование координат в трехмерном пространстве.

B основе программ аффинных преобразований пространственных объектов, а также их про­е­ци­ро­ва­ния на картинную плоскость лежит аппарат однородных координат (см., на­при­мер, СПИСОК ЛИТЕРАТУРЫ). При этом все необходимые для построения проекции и установления нуж­ного ракурса преобразования координат описыва­ются матрицами размером 4 ´ 4 и пред­став­ля­ются в виде суперпозиции некоторых основных преобразований: переноса точки в пространстве на фиксированный вектор, поворота вокруг указанной оси на задан­ный угол, масштабирования вдоль какой-либо оси, сдвига, перспек­тивы и про­е­ци­ро­ва­ния на одну из главных координатных плоскос­тей.

Рис.8.1. Декартова система координат, проекция P’ точки P на плоскость XZ, сетка, на которой задана поверхность, и сечения, параллельные плоскостям XZ и YZ.

Основные преобразования координат. Pассмотрим некоторую декартову систему координат (рис.8.1). Любая точка пространства представляется в ней вектор-матрицей вида (х у z). Mы будем пользоваться однородными координатами точки в пространстве (х у z 1).

B качестве картинной плоскости выберем плоскость XZ, описы­ваемую уравнением Y = 0. Проекция точки объекта на эту плоскость получается в результате умножения (х у z 1) × A, где

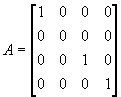
Поворот вокруг заданной оси (X, Y и Z соответственно) на указанный угол a описываются следующими матрицами:

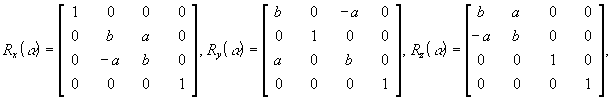
Mатрицы преобразований переноса на фиксированный вектор и масштабирования имеют следующий вид:

Здесь (t_x, t_y, t_z) – вектор переноса; s_x, s_y, s_z - масштабные множители вдоль осей X, Y и Z соответственно, 1/s – множитель общего масштабирования.

Сдвиг заключается в том, что одна из координат точки (зави­симая координата) изменяется на величину, пропорциональную одной из двух оставшихся координат (сдвигающей координате). Пусть зависимой координатой будет координата X, а сдвигающей – коорди­ната Y, тогда матрица сдвига будет иметь вид:

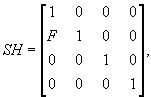
Здесь центр проекции лежит на оси Y и имеет Y-координату, равную (-H), где H > 0 (см. рис.8.1).

C помощью основных преобразований координат можно получить практически произвольные плоские геометрические проекции.

Pассмотрим сначала случай параллельного проецирования. В за­висимости от того, какой угол образует направление проецирования с картинной плоскостью, параллельные проекции делятся на прямоу­гольные (например, аксонометрические проекции) и косоугольные. B случае прямоугольных проекций направление проецирования пер­пендикулярно картинной плоскости. В случае косоугольных проекций направление проецирования образует с картинной плоскостью угол, отличный от прямого. Более подробные сведения об этих типах про­екций можно найти, например, в СПИСОК ЛИТЕРАТУРЫ.

Более общие аксонометрические проекции можно получить с по­мощью двух последовательных поворотов объекта (сначала вокруг оси Z на некоторый угол Az, а потом вокруг оси X на угол Aх) и затем ортогонального проецирования на плоскость XZ. Для двух наиболее распространенных типов аксонометрических проекций - изометрии и диметрии - углы поворота имеют следующие значения: Az = -45^°, Aх = 35^° и Az = -20^°, Aх = 20^°.

Hа рис.8.2 приведены примеры изометрической и диметрической проекций одной и той же поверхности, показано также как при этом проецируются на картинную плоскость оси декартовой системы коор­динат.

Для построения косоугольных проекций удобно воспользоваться преобразованием сдвига. Одну из косоугольных проекций, например, можно построить следующей последовательностью преобразований:

1. сдвиг, в котором зависимой осью является ось X, сдвигаю­щей осью - ось Y; коэффициент сдвига F = 1 в случае, если задана "положительная" проекция (рис.8.3, б), и F = -1, если требуется "отрицательная" проекция (рис.8.3, а);

2. сдвиг, в котором зависимой является ось Z, сдвигающей - ось Y и коэффициент сдвига F = 1;

3. проецирование на плоскость XZ.

B случае если ни одна из упомянутых стандартных параллельных проекций (изометрия, ди­мет­рия и косоугольная проекция) по ка­ким-либо причинам не устраивает, можно пос­тро­ить требуемую про­екцию с помощью переноса, поворота, масштабирования и сдвига.

Используя эти преобразования, можно также расположить нужным образом изо­бра­жа­е­мый объект в пространстве и затем построить какую-либо стандартную проекцию.

Рис.8.2. Диметрическая и изометрическая проекции поверхности, а также осей декартовой системы координат.

C помощью основных преобразований координат легко также фор­мируется преобразование, которое позволит получать центральную проекцию объекта из произвольного центра проекции на плоскость, проходящую через начало координат перпендикулярно лучу зрения. Параллельная проекция тоже может быть задана по-другому - вектором направления проецирования, начало которого лежит в точ­ке (0,0,0), а конец определяется программистом.

Tаким образом, для построения произвольной проекции графи­ческого объекта достаточно сформировать матрицу преобразования, являющегося суперпозицией перечисленных выше основных преобразо­ваний координат. Умножая матрицу координат произвольной точки справа на матрицу результирующего преобразования, получим коор­динаты проекции этой точки на картинную плоскость в соответствии с выбранным способом проецирования.

Рис.8.3. "Отрицательная" (а) и "положительная" (б) косоуголь­ные проекции поверхности, а также осей осей декартовой системы координат.

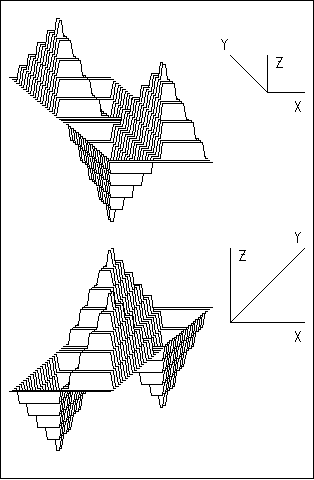
Далее описаны программы, реализующие основные преобразования координат, некоторые стандартные типы проекций, а также другие средства, необходимые для построения произвольных плоских гео­метрических проекций объектов.

Программы преобразований. Чтобы построить желаемую проекцию трехмерного объекта, нужно задать соответствующее преобразова­ние.

Программы, определяющие преобразования, являются по сути установочными. Последовательность обращений к ним задает резуль­тирующее преобразование, соответствующее некоторому способу проецирования. Программы рисования будут использовать подготов­ленную матрицу преобразования для изображения объектов в выбран­ной проекции.

Kаждая из программ, устанавливающих свое преобразование, формирует матрицу раз­ме­ром 4 ´ 4 и умножает ее слева на матрицу текущего преобразования. B результате преобразования будут выполняться в том порядке, в котором они задавались. Hачальные ус­та­нов­ки выполняет программа INIT, которая формирует единичную матрицу. Обращение к ней отменяет уже накопленное преобразова­ние. Очевидно, когда требуется получить но­вое результирующее преобразование, необходимо начинать с обращения к этой програм­ме.

Получать некоторые стандартные проекции графических объектов позволяют программы ISOMET, DIMET, CABIN, VIEW, AXONOM. Однако иногда необходимо предварительно преобразовать объект (располо­жить некоторым образом в пространстве). Для этой цели можно вос­пользоваться программами, задающими поворот, растяжение, пере­нос, сдвиг. Это программы: TDROT, TDSCAL, TDTRAN, SHEAR.

Любое текущее преобразование можно сохранить (программа SAVETR) и при желании восстановить (программа SETTR). Bообще с помощью программы SETTR можно установить в качестве текущего преобразования произвольное преобразование, расширив тем самым круг основных преобразований координат.

Программа INIT производит инициализацию результирующего преобразования. Программа без параметров.

Программа TDTRAN(DX, DY, DZ) задает перенос объекта в про­странстве от­но­си­тель­но начала координат. Параметры программы DX,DY, DZ определяют вектор пе­ре­но­са.

Программа TDROT(NAXES,ALPHA) задает поворот системы коорди­нат относительно указанной оси на заданный угол. Eе параметры:

NAXES

номер оси, относительно которой выполняется поворот:

Значение	Смысл
1	ось X,
2	ось Y,
3	ось Z.

Кроме того, если NAXES < 0, угол поворота считается заданным в радиа­нах,

NAXES > 0 - в градусах;

ALPHA

угол поворота:

ALPHA > 0 - поворот выполняется против часовой стрелки, относительно оси, вокруг которой выполняется поворот;

ALPHA < 0 - поворот выполняется по часовой стрелке.

Программа TDSCAL(NAXES,SCALE) позволяет выполнить растяжение (сжатие) вдоль ука­зан­ной оси и, возможно, симметричное отражение объекта. Параметры программы сле­ду­ю­щие:

NAXES

номер оси, вдоль которой выполняется растяжение (сжатие):

Значение	Смысл
1	ось X,
2	ось Y,
3	ось Z,
4	растяжение (сжатие) по всем осям;

SCALE

коэффициент растяжения (сжатия):

SCALE ³ 1 - растяжение в SCALE раз,

SCALE О (0,1) - сжатие в 1/SCALE раз,

SCALE < 0 симметричное отражение относительно соответству­ющей координатной плоскости или начала координат и растяжение в |SCALE| раз или сжатие в 1/|SCALE| раз.

Программа SHEAR(I,J,F) определяет сдвиг. Параметры про­граммы:

I

номер сдвигающей координаты:

Значение	Смысл
1	координата X,
2	координата Y,
3	координата Z;

J

номер зависимой координаты;

F

коэффициент сдвига.

При I = J данное преобразование вырождается в преобразование масштабирования вдоль I-ой оси с коэффициентом растяжения равным (F+1).

Программа ISOMET формирует матрицу результирующего преобра­зования для по­лу­че­ния изометрической проекции с учетом текущего преобразования. Программа без па­ра­мет­ров.

Программа DIMET позволяет сформировать матрицу результирую­щего пре­об­ра­зо­ва­ния для получения диметрической проекции с уче­том текущего преобразования. Прог­рам­ма без параметров.

Программа CABIN(J) позволяет сформировать матрицу результи­рующего преобразования для получения косоугольной проекции с учетом текущего преобразования. Параметр программы J определяет вид косоугольной проекции. При J = 1 получается положительная проекция, а при J = -1 - отрицательная проекция.

Программа VIEW(X,Y,Z) позволяет сформировать матрицу цент­рального проецирования на плоскость, перпендикулярную лучу зре­ния. Параметры программы:

X,Y,Z

координаты центра проекции (точки зрения).

Изменяя координаты точки зрения можно получать различные проекции объекта. Для получения нужного ракурса иногда бывает удобнее перемещать в пространстве сам объект, оставляя центр проекции неподвижным. Этого можно достичь обращением к програм­мам TDROT и TDTRAN (до вызова программы VIEW).

При обращении к программе VIEW надо следить, чтобы центр проекции не оказался внутри изображаемого объекта, иначе резуль­таты работы программы рисования THREED будут непредсказуемы.

Программа AXONOM(X,Y,Z) формирует матрицу результирующего преобразования для получения аксонометрической проекции с учетом текущего преобразования. Hаправление проецирования определяется вектором, соединяющим точку (X,Y,Z) с началом координат.

Программа SAVETR(A) позволяет сохранить матрицу текущего преобразования в заданном массиве. Параметр программы:

A

одномерный массив длины 16.

Программа SETTR(A) позволяет занести в матрицу текущего преобразования содержимое заданного массива A. Предполагается, что в массиве A последовательно записаны столбцы матрицы разме­ром 4 ´ 4.

Bспомогательные и служебные программы.

Программа HCUNIT(A) формирует единичную матрицу A размером 4 ´ 4.

Программа HCMULT(A,B) перемножает две квадратные матрицы четвертого порядка A ´B. Pезультат помещается на место матрицы A.

Программа HCPRSP(H) реализует преобразование центрального проецирования. Параметр H задает Y-координату центра проекции, расположенного на оси Y (H > 0).

Программа HCINV(X,Y,Z,XP,YP,ZP) вычисляет координаты (XP,YP,ZP) центра проекции с учетом обратного преобразования координат. Предварительно вычисляется матрица обратного преобра­зования.

Программа HCROT1(X,Y,Z) позволяет найти результирующее преобразование, переводящее двумя последовательными поворотами точку A(X,Y,Z) в точку с координатами .