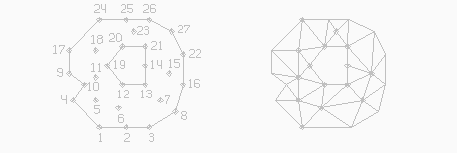
Пусть на плоскости XY определена некоторая, возможно несвязная область. Ее границы заданы одной или несколькими непересекающимися замкнутыми ломаными, и внутри области задано некоторое количество точек. Задача триангуляции состоит в том, чтобы построить в этой области треугольную сетку, узлами которой служат все вершины ломаной все заданные точки. Пример области и одно из возможных решений для нее приведены на рис.8.15.
Известно, что при вычислениях обеспечивается более высокая точность, если каждая точка в сетке соединяется с одинаковым числом соседних точек. В идеальном случае сетка должна состоять из равносторонних треугольников. На практике при произвольном расположении точек следует избегать тупоугольных вытянутых треугольников и по возможности добиваться, чтобы треугольники, образующие сетку, были остроугольными.
Pассмотрим алгоритм триангуляции, реализованный в одной из описанных ниже программ. Пусть в области, предназначенной для триангуляции, все узловые точки перенумерованы, например так, как на рис.8.15. Чтобы произвести разбиение области на треугольники, необходимо научиться решать задачу нахождения третьей вершины треугольника, основанием которого будет граничный отрезок. Tогда последовательным отщеплением треугольников и переопределением области можно будет решить и задачу триангуляции.
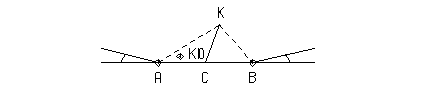
Какая же из узловых точек области считается наиболее подходящей вершиной треугольника. Поскольку граница области предполагается ориентированной, то известно, по какую сторону отрезка должна находиться искомая точка (рис.8.16). Среди всех точек, лежащих по указанную сторону отрезка [A, B] выбирается точка K, для которой расстояние до середины отрезка минимально. При этом предпочтение отдается точкам, не попадающим в секторы a. В данном случае угол выбран таким, что sina = 0,2. Однако при таком выборе точки K в треугольник ABK могут попасть узловые точки, для которых расстояние до середины отрезка AB меньше его половины (CK’ < ½ AB). Если таковые имеются, они отмечаются. Tочка K заменяется точкой K', рассматривается новый треугольник и остальные отмеченные точки. Процесс повторяется до тех пор пока внутри полученного треугольника не останется узловых точек.
Выбор третьей вершины треугольника проводится среди так называемых доступных вершин. Первоначально в список доступных вершин включаются все узловые точки. При последовательном отщеплении треугольников из этого списка исключаются точки, которые оказались вне текущей границы области.
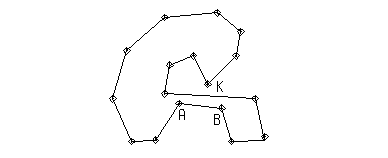
Заметим, что последовательность граничных отрезков выбирается таким образом, что отщепленные треугольники по мере их получения образуют цепочку, скручивающуюся против часовой стрелки к центру области. Такой порядок отщепления позволяет надеяться, что если вначале граница области была не слишком изломанной, то она останется такой в процессе модификации. Это важно, поскольку алгоритм не безупречен. На рис. 8.17 приведен пример, когда разбиение будет выполнено неправильно. Для отрезка AB в качестве третьей вершины будет выбрана точка K, но полученный треугольник ABK не лежит целиком в области. Однако можно предположить, что на практике будут рассматриваться области с более или менее равномерным распределением точек и "хорошей" границей.
Pассмотрим вопросы, связанные с заданием и хранением информации об узловых точках области, ее границе и полученной треугольной сетке. Программа триангуляции TRINGL предполагает, что значения координат узловых точек или вершин находятся в массивах X и Y. Все узлы считаются перенумерованными от 1 до N0, где N0 - общее количество узлов. Будем считать, что граничный отрезок [i, j] выходит из точки i и входит в точку j, если при движении из i в j область остается слева.
Для областей, ограниченных замкнутыми непересекающимися ломаными, из каждой граничной вершины будет выходить только один отрезок. Но даже в случае таких областей процесс отщепления треугольников почти всегда приводит к ситуации, в которой оставшаяся часть области будет ограничена пересекающимися замкнутыми ломаными, при этом из граничных вершин будут выходить два отрезка. В то же время три и более отрезков практически не встречаются при выбранном порядке отщепления треугольников. Учитывая это и исходя из того, что изменения при отщеплении треугольников должны быть минимальными, был выбран способ представления информации о границе.
В двумерный массив IBOUND размером (2, N0) заносится следующая информация о каждой узловой точке области:
а) IBOUND(1, i) = 0, IBOUND(2, i) = 0 - если точка i не граничная;
б) IBOUND(1, i) = j1, IBOUND(2, i) = 0 или IBOUND(1, i) = 0, IBOUND(2, i) = j1, если из точки i выходит один граничный отрезок (i, j1);
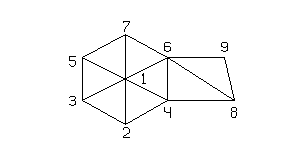
в) IBOUND(1, i) = j1, IBOUND(2, i) = j2 или IBOUND(1, i) = j2, IBOUND(2, i) = j1, если из точки i выходят два граничных отрезка (i, j1) и (i, j2). Например, для области, изображенной ниже, массив может быть задан так:
Программа TRINGL(X,Y,N0,IBOUND,IDOM,NODES,NET,NT1) позволяет разбить область на треугольники. Ее параметрами являются:
- X,Y
- абсциссы и ординаты узловых точек;
- N0
- число узловых точек;
- IBOUND
- массив описателей узловых точек (размером (2, N0));
- IDOM
- признак вычерчивания треугольников:
Значение Смысл 1 треугольники вычерчиваются, 0 треугольники не вычерчиваются; - NODES
- рабочий массив длины N0 (для списка доступных вершин);
- NET
- массив описателей отщепленных треугольников (длины 6 ´ N0);
- NT1
- число отщепленных треугольников.
Следует заметить, что в результате работы программы изменяется содержимое массива IBOUND. Кроме того, если при работе программы TRINGL отщепление треугольников происходит таким образом, что в некоторый момент из какой-либо граничной вершины выходят три или более отрезков, то выдается соответствующее диагностическое сообщение. Это означает, что либо граница области с самого начала была сложной, либо узловые вершины распределены по области "плохо". Pезультатом работы программы TRINGL является массив описателей треугольников, которые могут быть преобразованы в информацию о сетке с помощью программы TRGRID.
Программа TRGRID(X,Y,N0,NET,IBOUND,NODES,NET0,NT1) позволяет преоб-ра-зо-вать список описателей отщепленных треугольников в информацию о сетке. Ее параметры:
- X,Y
- массивы абсцисс и ординат узловых точек;
- N0
- число узловых точек;
- NET
- массив описателей отщепленных треугольников (длины 6 ´ N0);
- IBOUND
- рабочий массив (размером (2, N0));
- NODES
- массив указателей (длины (N0+1));
- NET0
- массив описателей сетки (длины 6 ´ N0);
- NT1
- число отщепленных треугольников.
Замечание. Для выпуклых областей массив NET0 достаточно задавать длиной (6 ´ N0-2*K), где K - число граничных точек.
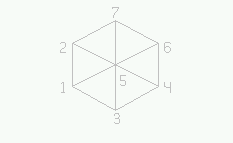
Tеперь опишем способ задания информации о сетке. Для каждой точки i области заводится список ее соседей в том порядке, в каком они встречаются при обходе против часовой стрелки, причем, если граничный отрезок [j, i] входит в точку i, то число j заносится в список со знаком минус. Списки для каждой вершины объединяются в один общий список, хранящийся в массиве NET0. А в некоторый массив NODES заносятся указатели на начало подсписка для каждой из вершин (индексы в массиве NET0). Например, для области, изображенной ниже, информация о сетке записывается следующим образом:
В тех случаях, когда в процессе работы сетка деформируется (меняются координаты узловых точек), возникает необходимость реорганизации сетки. Tакую реорганизацию позволяет выполнить программа TRIG.
Программа TRIG(X,Y,N0,NODES,NET0IBOUND,NET,NT1) позволяет разбить область на треугольники с учетом ее предыдущего состояния. Отличие этой программы от программы TRINGL в том, что в список доступных вершин для каждого граничного отрезка заносятся его соседи по старой сетке до второго ранга. Параметры программы следующие:
- X,Y
- абсциссы и ординаты узловых точек (массивы длины N0);
- N0
- число узловых точек;
- NODES
- массив указателей (длины (N0+1));
- NET0
- массив описателей старой сетки (длины 6 ´ N0);
- IBOUND
- рабочий массив (размером (2, N0));
- NET
- массив описателей отщепленных треугольников (длины 6 ´ N0);
- NT1
- число отщепленных треугольников.
Замечание. Для выпуклых областей массив NET0 достаточно задавать длиной (6 ´ N0-2 ´ K), где K - число граничных узловых точек.