Pассмотрим алгоритм построения центральной проекции поверхности, заданной фун-к-цией
z = f(х, у),
область определения которой в плоскости XY ограничена непересекающимися
ломаными линиями. В области определения строится треугольная сетка, в узлах которой заданы значения
функции f(х, у).
Эта функция приближается функцией
таким образом, что над каждым треугольником функция
f(х, у),
заменяется линейной по трем заданным значениям. Функция
представляет собой поверхность, сложенную из треугольных элементов, их
проекции и будут рассматриваться. В узловых точках значения функции
f(х, у)
и 
будут совпадать.
На взаимное расположение центра проекции, поверхности и картинной плоскости накладываются следующие ограничения:
а) точка (XV, YV) - проекция точки зрения на плоскость XY - должна лежать вне области определения функции;
б) проецируемая поверхность должна целиком находиться "перед лицом" наблюдателя, т. е. она должна полностью лежать по одну сторону от плоскости, параллельной картинной плоскости и проходящей через центр проекции.
Применяемый алгоритм удаления невидимых линий основывается на методе экранирования. Смысл этого метода заключается в том, что отмечается часть плоскости, занятая изображением, и при проведении новой линии рисуется только тот ее отрезок, который не попадает в эту уже занятую часть плоскости.
Следовательно, треугольные элементы поверхности должны быть упорядочены так, чтобы при рисовании последующие не закрывали предыдущих. Упорядочение элементов поверхности согласуется с упорядочением соответствующих треугольников в области определения функции и поэтому сначала изображается элемент, соответствующий тому треугольнику в области определения, который не закрывается никаким другим, затем - элемент, соответствующий треугольнику, который может закрываться лишь первым, и т. д. В условиях принятых ограничений на взаимное расположение центра проекции, картинной плоскости и поверхности такое упорядочение всегда существует (см. СПИСОК ЛИТЕРАТУРЫ).
Алгоритм упорядочения включает в себя алгоритм определения видимости отдельного треугольника. Будем называть сторону треугольника условно видимой, если угол между вектором внешней нормали и проекцией луча зрения больше 90°. В противном случае сторона называется условно невидимой. Tреугольник ABC (рис.8.18) с основанием AB, где AB - граничный отрезок, считается видимым и выбирается, если сторона AB условно видима, а две другие стороны либо условно невидимы, либо условно видимая сторона является граничной. При этом никакая из условно видимых граничных сторон не должна закрываться другими условно видимыми отрезками границы.
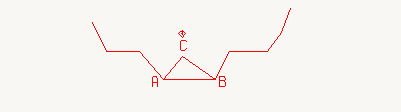
Пусть выбран видимый треугольник ABC. Выбор очередного видимого треугольника производится следующим образом. Если сторона AC была условно невидимой, то в первую очередь исследуется треугольник с основанием AC. Если он не подходит, то проверяем треугольники, лежащие от него слева и справа вдоль границы. Если и эти треугольники не подходят, еще раз сдвигаемся влево и вправо и так до тех пор, пока не найдем подходящий треугольник, либо не обойдем весь контур, которому принадлежит отрезок AC. В этом случае выбираем ближайший к точке (XV, YV) граничный отрезок и выполняем для него аналогичную операцию. Если же с самого начала сторона AC была условно видимой (при выборе предыдущего треугольника), то этот процесс начинаем с отрезка CB.
После того как сделан выбор треугольника в области определения, элемент поверхности, соответствующий этому треугольнику, изображается с учетом текущего экрана. Затем экран изменяется и осуществляется переход к выбору очередного треугольника. И так до тех пор, пока не будут исчерпаны все треугольники.
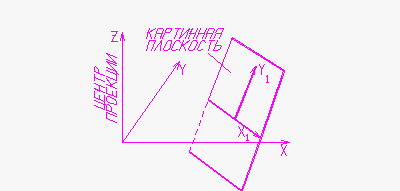
По мере рисования элементов поверхности требуется запоминать ту часть картинной плоскости, которая уже занята изображением. Для проведения необходимых вычислений нужно, прежде всего, выбрать на картинной плоскости некоторую систему координат x1y1 (рис.8.19). Направим ось x1 вправо (если смотреть от наблюдателя, стоящего вертикально в центре проекции) параллельно линии пересечения картинной плоскости с плоскостью xy. Ось y1 выберем перпендикулярной оси x1 и направленной в сторону возрастания координаты z.
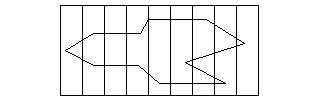
Для проведения экранирования в картинной плоскости определяется прямоугольник со сторонами, параллельными осям координат, внутри которого будет заключено изображение. Часть прямоугольника, которая уже занята изображением и в которой рисовать запрещается, запоминается следующим образом. Прямоугольник мысленно разбивается на равные части рядом вертикальных линий, назовем их экранными линиями (рис.8.20), т.е. вводится физическая сетка (ср. с пп.8.1.2, 8.2.1). На каждой экранной линии выделяются отрезки, принадлежащие той фигуре, которую нужно запомнить. Набор таких отрезков и является экраном, характеризующим эту фигуру.
Изображение поверхности строится последовательно по отдельным треугольникам в том порядке как описывалось выше. При рисовании каждого треугольника вычерчиваются те его стороны, которые до этого еще не рисовались (каждое ребро принадлежит двум треугольникам, но вычерчивается оно всего один раз). Вычерчивание происходит при неизменном экране, затем экран модифицируется. В экран заносятся отрезки экранных линий, которые оказываются внутри спроецированного треугольника. При этом, если необходимо, происходит склеивание нескольких отрезков в один.
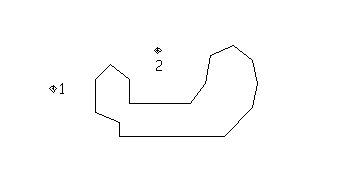
Для запоминания экрана служат два массива ISCR и SCRN. Mассив SCRN трехмерный, граничными значениями его индексов являются следующие величины: количество экранных линий, характеризующее частоту физической сетки, число отрезков на одной экранной линии и число 2. Для оценки максимального числа отрезков, которое может встречаться на экранных линиях, поступаем следующим образом (см. СПИСОК ЛИТЕРАТУРЫ). Спроецируем центр проекции на плоскость xy и подсчитаем, сколько раз луч, выходящий из построенной точки, может пересекать область определения, и к результату прибавим единицу. Число отрезков на каждой экранной линии не будет превышать полученной величины. Например, для области, показанной на рис.8.21, число отрезков на экранной линии не превысит трех для центра проекции в точке 1 и двух - в точке 2.
Число 2 в описании массива SCRN обусловлено тем, что запоминаются начало и конец отрезка. Поэтому k-й отрезок на i-й экранной линии записывается в этом массиве так: его координата Y меняется в пределах SCRN(I, K, 1) £ Y £ SCRN(I, K, 2). Другой массив, ISCR, одномерный, его длина определяется количеством экранных линий. В ISCR(I) запоминается число отрезков на i-й экранной линии. Перед началом рисования массив ISCR обнуляется.
При изображении очередного треугольника приходится искать точки пересечения его ребер с границей фигуры, внутри которой рисовать запрещено. Поэтому надо уметь восстанавливать границу фигуры по ее экрану. Чтобы понять как это делается, достаточно рассмотреть случай с двумя соседними экранными линиями.
а) Число отрезков на них одинаково
Tогда нижние отрезки соединяются между собой, верхние - между собой, остальные - аналогично.
б) Число отрезков различно
Построение границы идет как в а), только на той линии, где отрезков больше, (n-k) наименьших по длине отрезков в построении не участвуют.
Описать коротко сам процесс изображения отрезка с учетом экрана можно следующим образом. Будем говорить, что характеристика видимости точки на картинной плоскости равна 1, если точка лежит вне экрана, и 0 в противном случае. Для того чтобы нарисовать отрезок, нужно найти точки, где меняется характеристика видимости. Эти точки ищутся так. Экранными линиями весь отрезок разбивается на меньшие отрезки, для каждого из них определяются характеристики видимости его концов. Если они различны, то ищется точка пересечения отрезка с граничной линией экрана, в противном случае исследуется следующий малый отрезок и т. д.