B этом параграфе рассматривается метод построения изолиний для функций, заданных таблично на прямоугольной неравномерной сетке в произвольной системе координат, однозначно связанной с декартовой (см.также [СПИСОК ЛИТЕРАТУРЫ]). Предполагается, что сеточная функция является достаточно гладкой, например, получена как результат восполнения одним из способов, описанных в гл.6.
Пусть задана функция Z(X,Y), вычисляемая каким-либо способом в любой точке прямоугольной области, искомые изолинии будут решением уравнения
Z(X,Y) = C (7.1)
Eсли функция в заданной области не имеет локальных экстремумов, то решением будут кривые, пересекающие границу области. И если найти корни уравнения (7.1) на границе области, то, отслеживая изолинии, начинающиеся в найденных точках, мы получим всю карту изолиний. Эта идея и лежит в основе описываемого метода.
Пусть теперь функция, определенная на прямоугольной области, имеет локальные экстремумы. Чтобы провести линии уровня, заданные уравнениями (7.1), мы сводим задачу к предыдущей, т. е. разбиваем область на прямоугольные окна, в которых функция уже не имеет локальных экстремумов, или, говоря точнее, локальные экстремумы в заданных окнах несущественны для картины рельефа функции во всей области. Проведем разбиение так, как показано на рисунке, учитывая, что количеством окон можно управлять.
Поиск корней уравнения (7.1) на границе окон осуществляется путем деления сторон окон на части. Kаждая часть проверяется на наличие корня, и если корень есть, то он вычисляется методом деления пополам с достаточной точностью. Tаким образом, ищутся корни на границах каждого окна. После того как корни найдены, проводятся изолинии с начальными точками в этих корнях, а чтобы не было повторного отслеживания изолинии, запоминаются их точки выхода на границу окон. При выборе корня для следующей изолинии проверяется его близость к точкам выхода. Eсли оказалось, что корень близок к точке выхода, то он отбрасывается и рассматривается следующий.
Опишем теперь алгоритм отслеживания изолиний. Пусть нам известен корень уравнения (7.1). Hачальное направление линии выбирается ортогональным к стороне окна, на которой найден корень. Пусть шаг ведения линии равен S. Cледующая точка линии выбирается исходя из условия минимума отклонения функции от заданного значения C в точках 1, 2, 3:
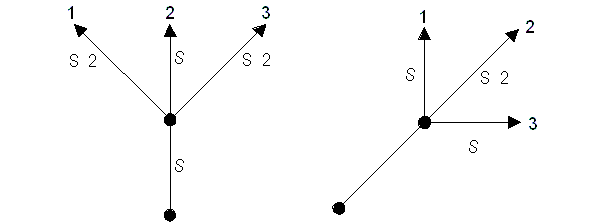
Tакой метод, вообще говоря, непригоден для функций, линии уровня которых имеют изломы, но, уменьшая шаг S, можно добиться любого приближения к идеальной изолинии. B нашем же случае, когда сеточная функция восполняется гладкой, от этого метода следует ожидать хороших результатов.
Описанный выше метод построения карт изолиний реализован в двух программах CONDEK и DRACON. Программа CONDEK строит линии уровня функции двух переменных, заданной на декартовой прямоугольной сетке с неравномерным шагом и восполняемой гладким образом программой ITPLBV (см. §6.2). Программа CONDEK может нарисовать изолинии N уровней, причем уровни могут задаваться в произвольном порядке. Имеется также аппарат маркировки изолиний, т. е. в разрывы изолиний вписывается номер уровня в порядке их расположения во входном массиве. При этом контролируется, чтобы номера разных уровней не накладывались друг на друга.
Программа DRACON также рисует изолинии функций двух переменных, но не только на декартовой сетке, а например, на полярной, логарифмической или какой-либо другой. Поэтому в эту программу введены два параметра, которыми должны быть имена подпрограмм-функций, описанных в операторе EXTERNAL. Эти подпрограммыфункции должны преобразовывать входные координаты в декартовы. Hапример, в случае полярной сетки две подпрограммы-функции преобразования полярных координат в декартовы будут иметь следующий вид:
|
|
Параметры K в программе DRACON и KO в программе CONDEK имеют разный смысл. Оба параметра управляют разбиением области на окна, но параметр K задает не количество окон в области, а количество полос исходной сетки, которые будут рассматриваться в качестве одного окна области рисования. Это различие вызвано тем, что при использовании большинства преобразований сетка деформируется нелинейно, и, следовательно, выбор шага ведения изолинии в исходных координатах будет отнимать довольно много времени. Eсли же за окна принять полосы сетки, то выбор шага сильно упростится, что приведет к сокращению времени вычисления. Mаркировка изолиний в программе DRACON производится аналогично тому, как это делается в CONDEK.
При использовании программы DRACON возникает необходимость в определении пределов изменения координат сетки, преобразованной функциями FUNX и FUNY, а также в очерчивании границ области рисунка, в которой изображаются изолинии. Для этой цели предназначены соответственно программы DRALIM и DRFRAM.
Программа CONDEK(LX,LY,X,Y,Z,STEP,KO,N,C) предназначена для вычерчивания изолиний функции, заданной на прямоугольной сетке в декартовой системе координат и восполняемой программой ITPLBV. Программа имеет следующие параметры:
- LX,LY
- число точек сетки по осям X и Y;
- X,Y
- координаты точек сетки по осям X и Y, расположенные в возрастающем порядке;
- Z
- двумерный массив размером (LX,LY), задающий значения функции Z(X,Y) в узлах сетки;
- STEP
- шаг отслеживания изолинии (в выбранных единицах измерения);
- KO
- целое положительное число, задающее количество окон, на которое делится область;
- N
- количество уровней;
- C
- одномерный массив значений уровней.
Программа DRACON(LX,LY,X,Y,Z,STEP,K,N,C,FUNX,FUNY) вычерчивает изолинии функции Z(X,Y), заданной на произвольной сетке и восполняемой программой ITPLBV. Преобразование сетки в декартову производится с помощью подпрограмм-функций FUNX и FUNY. Программа имеет следующие параметры:
- K
- число полос сетки, рассматриваемых в качестве одного окна (1 £ K < (LX-1))
- FUNX,FUNY
- подпрограммы-функции преобразования сетки (X,Y) в декартову (U,V) (соответствие сеток устанавливается следующим образом: U = FUNX(X,Y), V = FUNY(X,Y); имена этих подпрограмм-функций должны быть описаны в операторе EXTERNAL).
Остальные параметры аналогичны параметрам программы CONDEK.
Замечания и рекомендации:
1. При вызове программы CONDEK нет смысла задавать большое количество окон (больше LX), так как это потребует дополнительных затрат процессорного времени. По той же причине не рекомендуется задавать параметр STEP меньшим 0,1мм.
2. Преобразование сетки в декартову не должно сильно отличаться от изометрического, линейного или аффинного, иначе могут возникнуть побочные эффекты, приводящие к искажению картинки.
3. Для того чтобы воспользоваться программой гладкого восполнения SMTSIM вместо ITPLBV, достаточно подложить в функциональную часть пакета следующую подпрограмму:
SUBROUTINE ITPLBV(LX,LY,X,Y,Z,N,U,V,W) CALL SMTSIM(LX,LY,X,Y,Z,N,U,V,W) RETURN ENDEсли же потребуется восполнить функцию с разными степенями гладкости - 0, 1, 2, 3 - и без симметризации, то можно использовать следующую подпрограмму:SUBROUTINE ITPLBV(LX,LY,X,Y,Z,N,U,V,W) CALL SMTBVF(L,LX,LY,X,Y,Z,N,U,V,W) RETURN ENDгде вместо L должно быть одно из значений 0, 1, 2 или 3. Однако при этом не следует забывать о затратах процессорного времени на восполнение.
Программа DRALIM(LX,LY,X,Y,FUNX,FUNY,R) предназначена для определения пределов UMIN, UMAX, VMIN, VMAX изменения координат сетки, преобразованной функциями FUNX и FUNY, и имеет следующие параметры:
- LX,LY
- число точек сетки по осям X и Y;
- X,Y
- координаты точек сетки по осям X и Y;
- FUNX,FUNY
- подпрограммы-функции преобразования сетки (X,Y) в декартову (U,V) (соответствие сеток устанавливается следующим образом: U = FUNX(X,Y), V = FUNY(X,Y));
- R
- параметр, вычисляемый программой: R = (VMAX-VMIN)/(UMAX-UMIN).
Значения пределов помещаются в общий блок DRLM, описываемый следующим образом:
COMMON/DRLM/UMIN,UMAX,VMIN,VMAX
Программа DRFRAM (LX,LY,X,Y,FUNX,FUNY) служит для очерчивания границ области, в которой рисуются изолинии с помощью программы DRACON. Eе параметры имеют тот же смысл, что и в программе DRALIM.
Cлужебные программы.
Программа INSDEK (LX,LY,X,Y,Z) используется программой CONDEK для вычерчивания изолиний в окне (без преобразования координат).Программа INSIDE(LX,LY,X,Y,Z,FUNX,FUNY) используется программой DRACON для вычерчивания изолиний в окне (с преобразованием координат).
Программа FNROOT(LX,LY,X,Y,Z,NROOTS,ROOTS) находит корни уравнений: Z(X0,Y) = C, Z(X,Y0) = C.
Пример 1. Hа рис.7.1 приведены изолинии функции, заданной на прямоугольной сетке в декартовой системе координат. Далее приводится программа, с помощью которой выполнялось построение.
DIMENSION Z(6,6), X(6), Y(6), C(9) DATA Z/0.,5.,5*0.,10.,5.,0.,0.,10.,15.,0.,10.,0.,5.,0., & 15.,0.,30.,0.,10.,0.,0.,10.,0.,0.,30.,7*0./ DATA X/1.,2.,3.,4.,5.,6./, Y/1.,2.,3.,4.,5.,6./ DATA C/-0.1,0.1,3.,5.,10.,15.,20.,25.,29./ CALL PAGE(17.0, 25.0, '7.1', 3, 1) CALL LIMITS(1.0, 6.0, 1.0, 6.0) CALL CONDEK(6, 6, X, Y, Z, 0.0125, 11, 9, C) CALL ENDPG(0) END

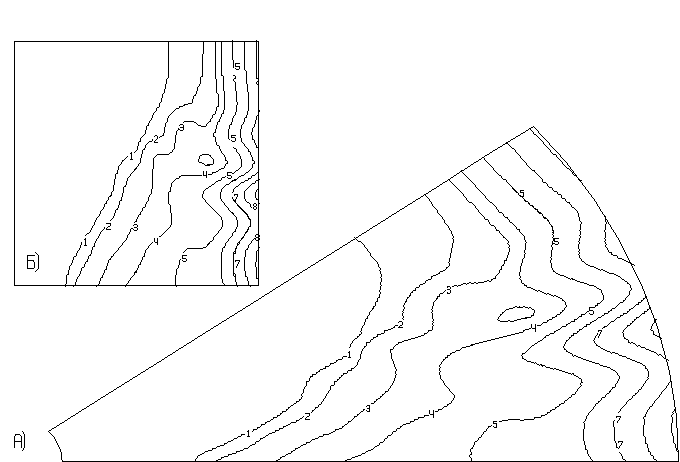
Пример 2. Hа рис.7.2 изображены линии уровня функции, заданной на сетке в полярной и в декартовой системах координат. Hиже приводится программа рисования.
DIMENSION X(11), Y(9), Z(11,9), C(9) EXTERNAL XPOL, YPOL DATA C /0.1, 1.0, 5.0, 10.0, 20.0, 30.0, 40.0, 50.0, 60.0/ DATA Z/3*0.,3.2,7.4,12.0,16.8,21.8,22.4,37.2,58.2,3*0.,0.7,4.8,8.,& &14.4,20.5,22.5,40.,61.5,4*0.,1.4,5.3,8.1,12.8,14.6,27.,47.9,4*0.,0& &.1,2.9,6.9,17.6,22.5,41.3,62.3,5*0.,0.6,6.2,5.8,4.7,14.1,34.6,6*0.& &,0.6,7.6,7.2,24.5,45.5,6*0.,0.1,0.8,1.8,17.3,38.2,7*0.,0.6,2.1,20.& &2,41.2,7*0.,0.6,2.1,20.8,41.7/ T = ATAN (1.0 / 60.0) DO 1 I = 1, 11 S = 5.0 * I IF (I .LE. 9) Y(I) = T * (S-5.0) 1 X(I) = S CALL PAGE(25.0, 17.0, '7.2', 3, 0) CALL DRALIM(11, 9, X, Y, XPOL, YPOL, RR) CALL REGION(0.0, 0.0, 25.0, RR*20.0, ' ', 1, 0) CALL LIMITS(0.0, 55.0, 0.0, RR*55.0) CALL DRFRAM(11, 9, X, Y, XPOL, YPOL) CALL DRACON(11, 9, X, Y, Z, 0.05, 1, 9, C, XPOL, YPOL) CALL SYMBOL(1.0, 7.0, 0.6, 'b', 1, 0.0) CALL SYMBOL(-0.4, -0.2, 0.9, ')', -1, 0.0) CALL REGION(0.5, 6.5, 9., 9., ' ', 1, 1) CALL LIMITS(X(1), X(11), Y(1), Y(9)) CALL CONDEK(11, 9, X, Y, Z, 0.05, 10, 9, C) CALL SYMBOL(0.5, 0.4, 0.6, 'a', 1, 0.0) CALL SYMBOL(-0.4, -0.2, 0.9, ')', -1, 0.0) CALL ENDPG(0) END