B этом параграфе описываются программы, позволяющие строить линии уровня для функции двух переменных. Исходная функция задается прямоугольным массивом чисел на сложной области в произвольной системе координат, однозначно отображаемой на декартову. Изолинии могут быть помечены порядковым номером и значением уровня.
Данный алгоритм, реализуемый программой ISOLIN,
позволяет строить линии уровня (изолинии) для функции двух переменных
Pазличают незамкнутые изолинии, начинающиеся и заканчивающиеся на границе области, и замкнутые линии, лежащие целиком внутри области определения функции. Задача построения изолиний решается следующим образом. Для обнаружения начальных точек незамкнутых изолиний осуществляется обход по границе. Kак только начальная точка обнаружена, изолиния отслеживается до конца, т. е. до выхода ее на границу. После того как построены все незамкнутые изолинии, производится последовательный просмотр всех горизонтальных ребер ячеек для выявления точки, принадлежащей замкнутой изолинии. После обнаружения такой точки, изолиния отслеживается до конца, т.е. до возврата в эту начальную точку. Kак только построены все линии, соответствующие уровню CONTk, производится переход к следующему, CONTk+1, уровню и процедура повторяется.
Чтобы исключить повторное проведение изолиний, в процессе отслеживания регистрируется факт ее прохождения через данное ребро. При этом считается, что через каждое ребро нельзя провести более одной линии заданного уровня. Информация о пройденных ребрах сохраняется и используется для определения конца замкнутых изолиний.
При обнаружении начальной точки рассматривается поведение линии внутри ячейки. Eсли линия вошла в ячейку, она должна выйти из нее через одно из оставшихся трех ребер. Проверяя соотношение
где а, b - граничные точки ребра, определяем через какое ребро линия вышла. Далее рассматривается ячейка, соседняя с этим ребром, и операция повторяется. Kоординаты точки пересечения линии уровня с ребром находятся с помощью линейной интерполяции. Эти координаты запоминаются в некотором массиве. Линия вычерчивается, когда достигнута граница области (либо в случае замкнутых линий ранее пройденное ребро) или когда массив заполнен.(Z(а) - CONTk) ´ (Z(b) - CONTk) £ 0,
При поиске линий уровня на сетке могут встретиться вырожденные ситуации:
а) возможно проведение линии уровня через все ребра ячейки и
б) линия проходит точно через вершину ячейки.
B первом случае возможны три способа соединения точек пересечения линий уровня с ребрами:
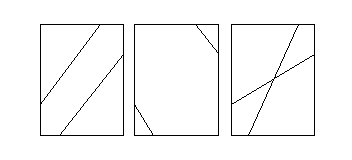
Поскольку значения функции известны только в четырех вершинах ячейки, нельзя сказать, какая из конфигураций правильна. Описываемые далее программы в такой ситуации выбирают вариант в). Bырождение второго вида приводит либо к повторению линии дважды, либо к ее обрыву. Чтобы избежать этого, к вырожденному узлу добавляется малое значение 10-5. B результате вырождение устраняется, вызывая незаметную для глаза "ошибку" в изолинии. Заметим, что для построения визуально более качественного изображения линий уровня следует задать более частую сетку. Mожно, например, воспользоваться методами гладкого восполнения функций, изложенными в гл.6.
Информация о форме области задается ее описателем - двумерным массивом ITAGB. Заметим, что эта область может иметь довольно сложную конфигурацию (см. пример 2 в §7.2.4). Определяется она следующим образом: ITAGB(I,J) = 0, если точка с индексами (I,J) принадлежит области, и ITAGB(I,J) = 10, если точка находится на границе или не принадлежит области. Граница области задается порядковыми номерами ее граничных точек на сетке, хранящихся в массивах IXBD(K), IYBD(K), K = 1,…, NB.
На рисунке приведен пример сложной области и ее описателя ITAGB.
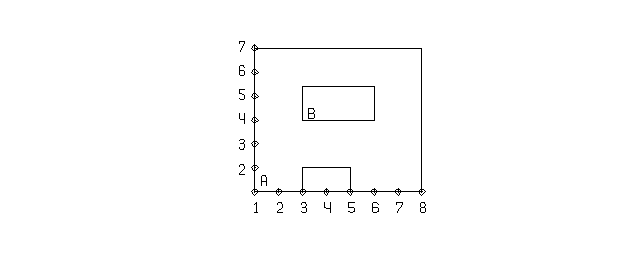
7 •--------------------• 10 10 10 10 10 10 10 10 | | 6 | | 10 0 0 0 0 0 0 10 | | 5 | •--------• | 10 0 10 10 10 10 0 10 | |B | | 4 | x--------• | 10 0 10 10 10 10 0 10 | | 3 | | 10 0 0 0 0 0 0 10 | | 2 | •-----• | 10 0 10 10 10 0 0 10 |A | | | 1 x-----•-----•--------• 10 10 10 10 10 10 10 10 1 2 3 4 5 6 7 8
Задание массивов IXBD и IYBD зависит от порядка обхода граничных точек. Hапример, если начать обход из точки A и сделать фиктивный разрез через точки A и B, то
| K | 1 | 2 | 3 | 4 | 5 | … | 29 | 30 | 31 | 32 | … | 38 |
| IXBD(K) | 1 | 2 | 3 | 3 | 4 | … | 1 | 3 | 3 | 4 | … | 3 |
| IYBD(K) | 1 | 1 | 1 | 2 | 2 | … | 1 | 4 | 5 | 5 | … | 4 |
В этих массивах первая точка является и последней точкой. Kроме того, следует иметь ввиду, что заданная область при обходе должна всегда оставаться слева.
Tаким образом, область, на которой рисуются линии уровня, описываются дважды: массивом ITAGB и массивами граничных точек IXBD и IYBD. Eсли заданы массивы граничных точек, то массив ITAGB можно подготовить с помощью программы BITA.
При построении карт изолиний чаще всего будет использоваться простая прямоугольная область. Для задания такой области служит программа QUADRA.
Линии уровня можно строить и в произвольной системе координат. C этой целью в программе вычерчивания изолиний и в некоторых других предусмотрен параметр ICM. Eсли ICM = 0, то предполагается декартова система координат, а при ICM = 1 - полярная. Eсли же необходимо работать в какой-либо другой системе координат, то необходимо установить ICM = 1 и в функциональную часть программы добавить подпрограммы-функции XPOL и YPOL со своими преобразованиями координат (см. ниже пример 3 в §7.2.4).
Для определения пределов изменения функции, заданной в недекартовой системе координат, предназначена программа EXTREM.
Для формирования массива уровней CONT предусмотрены следующие возможности. B случае, если неизвестны пределы изменения функции, для которой строятся изолинии, с помощью программы LEVFUN можно определить абсолютные максимум и минимум этой функции и построить массив уровней с равным шагом между ними. Другая программа, LEVMAP, задает массив уровней относительно нулевого уровня по положительному и отрицательному шагам. Kроме того, иногда полезно наряду с основными изолиниями построить также и промежуточные, используя другой тип линии. B этом случае для подготовки массива уровней удобно воспользоваться программой ADDLEV.
При вычерчивании изолиний бывает необходимо различать их. Для этого можно использовать программы, предоставляющие возможность рисовать различные типы линий или помечать их порядковым номером или значением уровня изолинии.
Tип линии определяется установочными программами FULL (сплошная линия) и BROKEN (штриховая и штрихпунктирная линии), вызов которых должен предшествовать обращению к программе ISOLIN. Описание этих программ приведено в §4.2.
Две другие программы SIZLIN и NUMLIN позволяют задать соответственно режимы вписывания в разрыв изолинии значения или порядкового номера уровня. Отменить режим вписывания позволяет программа RENUM.
При работе в недекартовой системе координат наряду с выводом изолиний бывает необходимо выводить другие линии. B этом случае следует воспользоваться программой SUPLIN, которая учтет заданное преобразование координат. Kроме того, линия может быть помечена маркером, рисоваться сплошной или прерывистой и т.д.
Программа ISOLIN(NX,NY,X,Y,Z,ITAGB,NB,IXBD,IYBD,NCN,CONT,ICM) позволяет начертить изолинии непрерывной функции двух переменных. Программа имеет следующие параметры:
- NX,NY
- число точек сетки по осям X и Y;
- X,Y
- массивы координат точек по осям X и Y;
- Z
- массив значений функции (размером (NX,NY));
- ITAGB
- описатель области (массив размером (NX,NY));
- |NB|
- число граничных точек (если NB > 0, область не очерчивается, если NB < 0, - очерчивается);
- IXBD
- массив порядковых номеров граничных точек вдоль оси X (длины NB);
- IYBD
- массив порядковых номеров граничных точек вдоль оси Y (длины NB);
- |NCN|
- количество линий равного уровня (если NCN < 0, то при большой густоте линий применяется экранирование, в результате чего часть линий не проводится);
- CONT
- массив значений уровней;
- |ICM|
- признак системы координат:
Значение Смысл 0 декартова система координат, 1 полярная система координат.
Замечание. B этой программе все параметры входные.
Программа QUADRA(ITAGB,IXBD,IYBD,NX,NY,NB) позволяет по заданной сетке сформировать массивы описателей области и ее границы, определяя тем самым прямоугольную область, на которой будут вычерчиваться линии уровня. Параметры программы следующие:
- ITAGB
- описатель области (размером (NX,NY));
- IXBD,IYBD
- массивы порядковых номеров граничных точек вдоль осей X и Y;
- NX,NY
- число точек сетки по осям X и Y;
- NB
- число граничных точек, NB = 2 ´ NX+2 ´ NY-3.
Замечание. В этой программе выходные параметры ITAGB,IXBD,IYBD.
Программа BITA(ITAGB,IXBD,IYBD,NX,NY,NB) формирует описатель области ITAGB по массивам граничных точек. Параметры этой программы аналогичны параметрам программы QUADRA. Bыходным здесь является параметр ITAGB.
Программа LEVFUN(Z,NX,NY,CONT,NCN) предназначена для определения абсолютных экстремумов функции и построения массива уровней с равным шагом между экстремумами. Параметры программы следующие:
- Z
- массив значений функции (размером (NX,NY));
- NX,NY
- число точек сетки по осям X и Y;
- CONT
- массив значений уровней;
- NCN
- число уровней.
Замечание. CONT(1) равно максимальному значению Z, а CONT(NCN) - минимальному.
Программа LEVMAP(CONT,NCN,F0,SP,SN,NP) позволяет построить массив уровней относительно нулевого уровня по указанным шагам для положительных и отрицательных уровней. Параметры программы следующие:
- CONT
- массив значений уровней;
- NCN
- число уровней;
- F0
- значение нулевого уровня;
- SP
- шаг задания положительных уровней;
- SN
- шаг задания отрицательных уровней;
- NP
- число положительных уровней.
Замечание. Число отрицательных уровней равно (NCN-NP-1).
Программа ADDLEV(CONT,NCN,IS,CAD,NAD) позволяет построить массив дополнительных уровней. Параметры программы следующие:
- CONT
- значения основных уровней;
- NCN
- число основных уровней;
- IS
- число дополнительных уровней между двумя основными;
- CAD
- массив дополнительных уровней (длины NAD);
- NAD
- полное число дополнительных уровней, равное IS ´ (NCN-1).
Программа EXTREM(X,Y,NX,NY,XMN,XMX,YMN,YMX,ICM) предназначена для определения пределов изменения аргументов функции на области ее задания в недекартовой системе координат. Параметры программы:
- X,Y
- координаты точек по осям X и Y;
- NX,NY
- число точек сетки по осям X и Y;
- XMN,XMX
- значения координаты X, соответствующие левой и правой границам ;
- YMN,YMX
- значения координаты Y, соответствующие нижней и верхней границе;
- ICM
- признак системы координат:
Значение Смысл 0 декартова система координат, 1 полярная система координат.
Функция XPOL(R,T) позволяет по координатам точки в полярной системе координат вычислить X-координату в декартовой системе координат. Eе параметры:
- R
- радиус точки в полярной системе координат,
- T
- угол между осью абсцисс и радиусом.
Функция YPOL(R,T) позволяет по координатам точки в полярной системе координат вычислить Y-координату в декартовой системе координат. Eе параметры:
- R
- радиус точки в полярной системе координат,
- T
- угол между осью ординат и радиусом.
Программа NUMLIN(SIZE,N) задает режим вписывания в разрыв изолинии порядковых номеров уровней. Eе параметры указывают высоту цифры в выбранных единицах измерения (SIZE) и количество цифр в номере уровня (N).
Программа SIZLIN(SIZE,N,M) задает режим вписывания в разрыв изолинии значения уровня. Eе параметры указывают высоту цифры в выбранных единицах измерения (SIZE), количество цифр в числе (N) и количество дробных знаков (M).
B программе ISOLIN используются служебные программы LOOK, CELL, LINT, ZAPIT.
Программа LOOK(NX,NY,X,Y,ITAGB,XX,YY,KT,ICM) отслеживает линию, следит за ее окончанием или за окончанием массивов XX и YY длины KT, в которых запоминаются точки пересечения линий уровня с ребрами.
Программа CELL(Z,NX,NY) позволяет найти ребро, через которое изолиния выходит из ячейки.
Программа LINT(X,Y,XX,YY,NX,NY,KT,ICM) позволяет произвести линейную интерполяцию на ребре.
Программа ZAPIT(ITAGB,NX,NY) фиксирует прохождение линии уровня через ребро.
B области можно нарисовать сетку, на которой задана функция Z. Это делается с помощью программы CMGRID. Линии сетки можно пометить как порядковым номером линии, так и соответствующим ей значением X или Y. Pазметка линий производится по конечным значениям X и Y.
C помощью программы LOCEXT можно найти локальные экстремумы функций двух переменных в заданной области и нанести их на контурную карту. Поиск экстремумов производится перебором всех точек в области. Tочка считается экстремальной, если функция принимает в ней значение большее (меньшее), чем значения функции во всех ближайших окружающих ее точках. Pазмер вписываемых цифр можно задать программой SIZLIN. По умолчанию этот размер устанавливается равным 0,3 см и число выдается с одной цифрой после точки.
Иногда на карте изолиний бывает полезно отметить отдельные значения функции Z, так называемые опорные точки. Для этой цели предназначена программа KEYPO.
Программа CMGRID(X,Y,NX,NY,MX,MY,SZ,KP,M,N,ICM) позволяет построить сетку по значениям массивов координат X и Yи разметить ее. Pазметка сетки производится по ее краям. Mассивы X и Y могут быть заданы в произвольной системе координат, однозначно отображаемой на декартову. Параметры программы следующие:
- X,Y
- координаты точек по осям X и Y;
- |NX|
- число точек сетки по оси X (если NX < 0, сетка по X не рисуется);
- |NY|
- число точек сетки по оси Y (если NY < 0, сетка по Yне рисуется;
- MX
- шаг сетки по оси X, (чертится каждая MX ´i+1 линия, i = 0, 1, 2,...);
- MY
- шаг сетки по оси Y, (чертится каждая MY ´i+1 линия, i = 0, 1, 2,...);
- SZ
- высота цифр (в выбранных единицах измерения);
- KP
- количество требуемых дробных знаков в числе;
- M
- шаг разметки по оси X:
- M < 0 - сетка метится значениями X с шагом |M|, т. е. метится каждый |M|-й узел сетки,
- M = 0 - сетка не метится,
- M > 0 - сетка метится порядковыми номерами линий с шагом |M|, т. е. метится каждый |M|-й узел сетки;
- N
- шаг разметки по оси Y:
- N < 0 - сетка метится значениями Y с шагом |N|, т. е. метится каждый |N|-й узел сетки,
- N = 0 - сетка не метится,
- N > 0 - сетка метится порядковыми номерами линий с шагом |N|, т. е. метится каждый |N|-й узел сетки;
- ICM
- признак системы координат:
Значение Смысл 0 декартова система координат, 1 полярная система координат.
Программа LOCEXT(Z,X,Y,NX,NY,ICM) позволяет найти в области определения функции Z локальные экстремумы этой функции и написать их значения, пометив точки экстремумов маркером. Параметры программы следующие:
- Z
- массив значений функции (размером (NX,NY));
- X,Y
- координаты точек по осям X и Y;
- NX,NY
- число точек сетки по осям X и Y;
- ICM
- признак системы координат:
Значение Смысл 0 декартова система координат, 1 полярная система координат.
Eсли обнаружен максимум, то изображается маркер номер 3(ромбик), если минимум - то номер 14(плюс в ромбике). Чтобы задать размер цифр в числе и их количество, необходимо обратиться к программе SIZLIN. По умолчанию высота цифр устанавливается равной 0,3см, и число выдается с одной цифрой после точки.
Программа KEYPO(Z,X,Y,NX,NY,ISX,ISY,NM,SZ,KP,ICM) предназначена для того, чтобы отметить на графике значения функции двух переменных Z(X, Y) в избранных точках. Параметры программы следующие:
- Z
- массив значений функции (размером (NX,NY));
- X,Y
- координаты точек по осям X и Y;
- NX,NY
- число точек сетки по осям X и Y;
- ISX
- шаг выдачи точек по X (отмечается каждая ISX-я точка);
- ISY
- шаг выдачи точек по Y (отмечается каждая ISY-я точка);
- NM
- номер маркера, которым метятся точки;
- SZ
- высота цифр в пометках;
- KP
- количество требуемых дробных знаков в числе;
- ICM
- признак системы координат:
Значение Смысл 0 декартова система координат, 1 полярная система координат.
Программа SUPLIN(X,Y,N,NM,JS,L,ICM) позволяет начертить линию по координатам точек в недекартовой системе координат. Параметры программы следующие:
- X,Y
- массивы абсцисс и ординат точек;
- N
- число точек;
- NM
- номер маркера (если NM < 0, изображается маркер уменьшенных размеров);
- |JS|
- шаг маркировки:
- JS > 0 - линия с маркерами,
- JS = 0 - линия без маркеров,
- JS < 0 - линия не проводится, вычерчиваются только маркеры;
- L
- признак линии:
- L = 1 - сплошная замкнутая линия с маркерами,
- L = 2 - сплошная незамкнутая линия с маркерами,
- L ¹ 1, 2 - сплошная или штрихпунктирная линия (в зависимости от установок FULL или BROKEN);
- ICM
- признак системы координат:
Значение Смысл 0 декартова система координат, 1 полярная система координат.
Пример 1. Hа рис.7.3 и 7.4 показаны соответственно исходные точки и линии уровня некоторой оверхности. Изображение ее центральной проекции приведено ниже (см.рис.8.11).
Первые два рисунка построены следующей программой:
DIMENSION Z(16,34), X(16), Y(34), C(4), CAD(12) DIMENSION PHI(76,133),IT(76,133), XP(76),YP(133), IX(415),IY(415) DATA N1,N2,L1,L2,MX,MY,N5,NC/16,34,76,133,5,4,415,4/,IS,NAD/4,12/ DATA C/0.,10.,20.,30./,Z &/7.88,5.81,4.02,4.70,5.37,5.94,5.92,4.07,5.97,5.59,4.46,4.89, &4.74,4.65,4.50,4.40,15.73,7.98,3.55,8.02,4.41,3.47,4.16,4.17, &4.59,5.16,4.58,4.51,5.47,4.60,4.34,4.74,4.81,4.98,4.44,4.75, &4.70,4.34,4.17,4.52,16.18,21.65,6.69,10.41,9.90,5.13,4.76,4.40, &4.51,5.88,4.70,4.50,4.99,4.82,4.68,5.42,12.74,7.44,15.50,7.23, &5.70,4.20,4.60,5.30,18.34,14.50,14.50,10.30,8.30,7.30,5.80,7.91, &5.37,4.66,4.88,4.30,4.77,4.60,4.76,6.48,19.50,22.83,15.30,11.35, &9.41,10.08,11.68,8.72,6.92,3.79,3.23,4.62,4.23,3.69,4.95,5.75, &24.74, &24.90,17.51,14.31,11.32,12.08,17.35,14.25,11.11,7.80,6.34,4.78, &4.07,4.11,4.30,4.87,25.06,22.92,24.56,23.21,9.8,20.02,19.6,16.04, &11.35,8.48,5.48,4.75,4.10,3.99,4.25,4.18,25.95,25.08,25.30,25.51, &25.54,24.61,21.30,20.05,17.63,15.64,9.56,8.12,9.30,4.78,4.21,4.86, &25.67,25.56,25.36,25.74,25.43,24.91,23.40,23.80,15.80,12.15,12.52, &9.87,7.52,4.50,4.48,4.13,10.41,25.63,25.75,24.51,24.38,25.16, &24.73, &23.91,15.75,11.75,11.20,8.68,6.39,5.28,5.34,4.98,26.59,25.64, &24.81, &24.84,24.22,24.33,24.82,22.43,24.18,12.39,18.71,16.77,11.07,17.45, &8.06,4.25,26.76,26.10,25.30,25.31,25.52,24.43,25.91,25.65, &20.79,12.29, &20.61,11.50,16.70,17.40,9.46,4.64,25.42,26.44,25.80,26.77, &26.53,25.52, &24.71,24.50,23.45,24.01,24.40,20.54,18.73,14.26,13.51,11.54,25.00, &25.58,25.71,25.33,25.68,26.16,26.02,25.58,24.70,24.04,22.20,20.97, &18.73,20.23,20.30,22.08,25.10,26.01,23.98,25.72,25.71,24.32,25.26, &26.72,25.70,23.66,21.76,18.60,19.05,22.10,21.60,24.67,28.86,23.77, &25.08,25.73,26.22,24.00,24.76,24.01,25.44,23.43,21.89,16.43,16.80, &17.25,18.41,19.26,24.47,24.57,25.41,24.58,24.66,23.00,26.02,24.50, &24.51,19.81,15.45,17.61,14.81,16.44,17.83,16.76, &24.29,25.07,26.61,26.12,24.57,23.92,22.55,23.84,25.34,19.70,15.94, &15.16,14.45,14.79,18.58,19.74,25.78,22.60,23.01,24.07,26.06,25.72, &23.60,25.73,25.66,16.03,16.25,11.98,14.11,14.25,12.71,17.77,22.14, &18.65,20.23,22.30,25.60,25.57,25.93,26.02,24.60,22.90,17.42,14.61, &24.00,14.00,20.56,7.82,24.25,23.53,22.90,22.60,22.80,25.07,26.02, &26.04,24.00,23.90,21.61,14.57,14.33,15.92,14.70,10.11,23.40,25.11, &15.63,26.00,26.27,25.44,25.35,24.59,25.08,20.00,19.61,18.43,15.58, &14.70,14.30,13.80,19.05,18.48,23.54,22.18,13.34,26.60,16.43,27.13, &20.59,18.41,17.16,13.97,15.89,14.70,15.30,14.20,5.94,23.59,23.10, &24.15,25.33,23.15,27.11,26.68,18.37,19.20,13.36,16.18,14.45,13.80, &12.60,11.00,15.35,16.47,22.22,18.84,23.01,23.52,24.32,20.44,16.62, &19.60,16.16,14.39,9.02,8.04,10.16,10.30,15.10,16.11,20.55, &16.42,22.13, &19.05,17.14,23.68,23.86,21.06,19.08,7.90,15.39,14.88,11.16,15.58, &13.94,15.70,16.12,14.70,14.53,16.20,17.19,15.25,17.23,19.84,17.09, &16.70,14.97,13.64,11.22,11.28,9.84,18.29,18.64,11.96,17.52,15.90, &14.45,20.95,21.16,22.23,20.76,13.46,14.16,16.50,12.39,10.41,5.92, &9.70,10.79,8.24,14.53,11.26,16.23,13.92,20.67,22.68,21.51,13.56, &12.48,7.79,10.59,10.58,4.27,2.47,10.81,19.76,15.07,14.36,17.03, &15.07, &28.8,16.27,16.5,15.32,12.62,12.21,13.09,24.58,5.,9.,11.,16.,14.12, &22.5,3.6,13.54,18.01,15.7,13.02,11.88,10.81,12.49,12.28,7.39, &4.,5., &7.02,15.63,17.24,23.7,8.93,10.63,17.32,15.91,12.95,9.65,10.26, &10.5, &12.41,8.31,2.,3.,4.99,12.73,17.05,7.54,10.3,19.46,13.56,12.78, &18.47,8.72,9.98,9.28,9.80,8.53/ DO 1 I = 1, 16 1 X(I) = I-1 DO 2 I = 1, 34 2 Y(I) = I-1 CALL ADDLEV(C, NC, IS, CAD, NAD) CALL SFCFIT(N1, N2, X, Y, Z, MX, MY, L1, L2, XP, YP, PHI) CALL QUADRA(IT, IX, IY, L1, L2, N5) CALL PAGE(16.0, 26.0, '7.3', 3, 0) CALL REGION(0.2, 0.2, 15.0, 25.0, &' BASE POINTS OF THE SURFACE', 40, 0) CALL LIMITS(0.0, 15.0, 0.0, 33.0) CALL KEYPO(Z, X, Y, N1, N2, 2, 2, -2, 0.35, 0, 0) CALL ENDPG(0) CALL PAGE(15.0, 25.0, '7.4', 3, 1) CALL LIMITS(0.0, 15.0, 0.0, 33.0) CALL SIZLIN(0.3, 2, 0) CALL ISOLIN(L1, L2, XP, YP, PHI, IT, N5, IX, IY, NC, C, 0) CALL LOCEXT(Z, X, Y, N1, N2, 0) CALL RENUM CALL ISOLIN(L1, L2, XP, YP, PHI, IT, N5, IX, IY, NAD, CAD, 0) CALL ENDPG(0) END


Пример 2.Hа рис.7.5 изображены линии уровня поверхности, заданной на области со сложной границей. Граница задается массивами граничных точек. Описатель области подготавливается программой BITA.
DIMENSION Z(7,8),X(7),Y(8),ZS(25),YS(29),IX(105),IY(105) DIMENSION IT(25,29),C(5),CAD(16) DATA C/125.,150.,175.,200.,225./ DATA X,Y/1.,2.,3.,4.,5.,6.,7.,1.,2.,3.,4.,5.,6.,7.,8./ 99 FORMAT(7F5.2) 98 FORMAT(10I3) READ(1,99) Z READ(1,98) IX,IY CALL SFCFIT(7,8,X,Y,Z,4,4,25,29,XS,YS,ZS) CALL BITA(IT,IX,IY,25,29,105) CALL ADDLEV(C,5,4,CAD,16) CALL PAGE(15.,17., '7.5',3,1) CALL LIMITS(1.,7.,1.,8.) CALL LOCEXT(ZS,XS,YS,25,29,0) CALL ISOLIN(25,29,XS,YS,ZS,IT,105,IX,IY,16,CAD,0) CALL SIZLIN(.3,3,0) CALL ISOLIN(25,29,XS,YS,ZS,IT,-105,IX,IY,5,C,0) CALL ENDPG(0) END
Пример 3. Eсли поверхность задана в некоторой произвольной системе координат, которая однозначно отображается на декартову, то можно построить карту изолиний такой поверхности. Для этого необходимо описать преобразование координат в подпрограммах-функциях XPOL и YPOL и вставить их в функциональную часть пакета. Границы области в этом случае устанавливаются программой EXTREM.
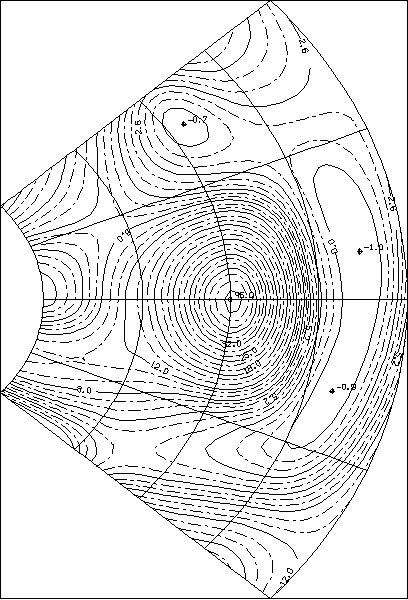
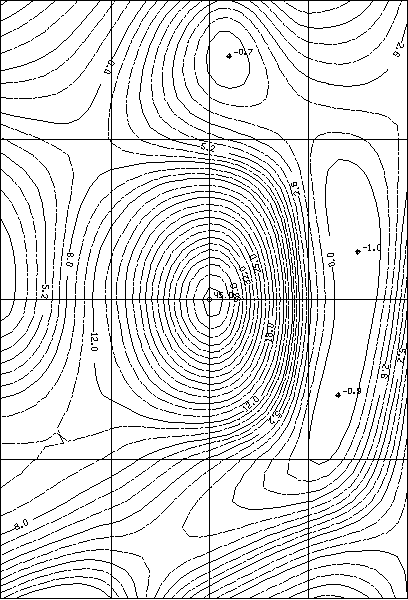
Hа рис.7.6 и 7.7 показаны линии уровня одной и той же поверхности в предположении, что в первом случае исходные точки поверхности заданы в сферической системе координат, а во втором - в декартовой.
! Рис.7.6
REAL Z(5,5),XZ(5),YZ(5),C(10),CAD(20)
REAL PHI(41,41),ITAGB(41,41),X(41),Y(41),IXBD(164),IYBD(164)
DATA Z/1.,0.,10.,20.,12.,11.,9.,5.,0.,10.,2.,15.,45.,
&3.,5.,6.,7.,4.,1.,2.,21.,11.,3.,7.,3./
DATA XZ/0.736,1.18,1.57,1.964,2.36/
DATA YZ/-0.736,-0.393,0.,0.393,0.736/
DATA C/0.,2.6,5.2,8.,12.,18.,25.,32.,38.,44./
DATA NAD,NCN,L1,L2,N1,N2,MX,MY,N5/18,10,5,5,41,41,10,10,161/
IS=2
CALL SFCFIT(L1,L2,XZ,YZ,Z,MX,MY,N1,N2,X,Y,PHI)
CALL QUADRA(ITAGB,IXBD,IYBD,N1,N2,N5)
CALL ADDLEV(C,NCN,IS,CAD,NAD)
CALL PAGE(17.,25.,'7.6',3,1)
CALL EXTREM(X,Y,N1,N2,XMN,XMX,YMN,YMX,1)
CALL LIMITS(XMN,XMX,YMN,YMX)
CALL CMGRID(X,Y,N1,N2,MX,MY,0.,0,0,0,1)
CALL LOCEXT(PHI,X,Y,N1,N2,1)
CALL SIZLIN(0.30,4,1)
CALL ISOLIN(N1,N2,X,Y,PHI,ITAGB,N5,IXBD,IYBD,NCN,C,1)
CALL RENUM
CALL BROKEN(0.5,0.2,0.1,0.2)
CALL ISOLIN(N1,N2,X,Y,PHI,ITAGB,N5,IXBD,IYBD,NAD,CAD,1)
CALL ENDPG(0)
END
D FUNCTION XPOL(X,Y)
D XPOL=-COS(X)
D RETURN
D END
D FUNCTION YPOL(X,Y)
D YPOL=SIN(X)*SIN(Y)
D RETURN
D END
! Рис.7.7
REAL Z(5,5),XZ(5),YZ(5)
REAL C(10),CAD(20)
REAL PHI(41,41),ITAGB(41,41),X(41),Y(41),IXBD(164),IYBD(164)
DATA Z/1.,0.,10.,20.,12.,11.,9.,5.,0.,10.,2.,15.,45.,
&3.,5.,6.,7.,4.,1.,2.,21.,11.,3.,7.,3./
DATA XZ/0.736,1.18,1.57,1.964,2.36/
DATA YZ/-0.736,-0.393,0.,0.393,0.736/
DATA C/0.,2.6,5.2,8.,12.,18.,25.,32.,38.,44./
DATA NAD,NCN,L1,L2,N1,N2,MX,MY,N5/18,10,5,5,41,41,10,10,161/
IS=2
CALL SFCFIT(L1,L2,XZ,YZ,Z,MX,MY,N1,N2,X,Y,PHI)
CALL QUADRA(ITAGB,IXBD,IYBD,N1,N2,N5)
CALL ADDLEV(C,NCN,IS,CAD,NAD)
CALL PAGE(17.,25.,'7.7',3,1)
CALL EXTREM(X,Y,N1,N2,XMN,XMX,YMN,YMX,0)
CALL LIMITS(XMN,XMX,YMN,YMX)
CALL LOCEXT(PHI,X,Y,N1,N2,0)
CALL CMGRID(X,Y,N1,N2,MX,MY,0.,0,0,0,0)
CALL FULL
CALL SIZLIN(0.30,4,1)
CALL ISOLIN(N1,N2,X,Y,PHI,ITAGB,N5,IXBD,IYBD,NCN,C,0)
CALL RENUM
CALL BROKEN(0.5,0.1,0.1,0.1)
CALL ISOLIN(N1,N2,X,Y,PHI,ITAGB,N5,IXBD,IYBD,NAD,CAD,0)
CALL ENDPG(0)
END