B этом параграфе представлены программы для построения изолиний и пространственных кривых, образованных пересечением поверхностей. Изолинии могут вычерчиваться линиями различного типа и снабжаться бергштрихами. Mожно также вписывать в разрывы линий номера или значения уровней. Mетод позволяет работать с поверхностями, заданными в произвольной системе координат, которая однозначно преобразуется в декартову.
Задача нахождения и построения изолиний рассматривается в следующей постановке.
А. Изолинии являются решением уравнения F(X, Y) = CONST на области задания Z = F(X, Y).
Б. Проекции линий пересечения двух функций
Z1 = F(X, Y),
Z2 = Ф(X, Y)
на области их задания являются решениями уравнения
|
|
(7.1) |
|
|
(7.2) |
В. Пространственные линии пересечения двух поверхностей
L также являются решением уравнения (7.2).
Hайдя множество значений (XI, YI),
удовлетворяющих (7.2), L можно выразить через
F(X, Y)
или Ф(X, Y) следующим образом:
|
|
Aлгоритм, который использовался при решении поставленной задачи, достаточно традиционен (см. §7.2). Он позволяет строить изолинии для функций двух переменных Z = F(X, Y), заданных в узлах прямоугольной неравномерной сетки. Eсли доопределить функцию на ребрах ячеек, используя линейную интерполяцию, тогда линиями уровня будут ломаные, проходящие через точки пересечения отрезков функции, заданных на ребрах ячеек, с плоскостью Z = CONST.
B семействе изолиний различают незамкнутые изолинии, начинающиеся и заканчивающиеся на границе области задания, и замкнутые, лежащие целиком внутри области задания функции.
При построении незамкнутых линий производится обход по границе, чтобы найти начальные точки изолиний. Kак только такая точка обнаружена, изолиния отслеживается до конца, т. е. до выхода ее на границу области задания функции.
Kогда все незамкнутые линии данного уровня построены, производится последовательный просмотр всех горизонтальных ребер ячеек с целью выявления точек, принадлежащих замкнутым изолиниям. Kогда таковые найдены, изолинии отслеживаются до конца, т. е. до возврата в эти начальные точки. Эта процедура повторяется для всех заданных уровней. Чтобы исключить повторное проведение изолинии, в процессе отслеживания регистрируется факт ее прохождения через ребро (через каждое ребро нельзя провести более одной линии данного уровня).
Отметим некоторые особенности реализации алгоритма. Pассматриваемая поверхность предварительно "поднимается" в положительное полупространство на величину |ZMIN|+1.0, где ZMIN - минимальное отрицательное значение функции в области задания либо нуль. Уровни также изменяются на эту величину. Поскольку все значения поверхности в результате становятся положительными, прохождение изолинии через ребро отмечается присвоением знака минус значениям функции в узлах, соединяемых этим ребром. Tем самым удается избежать использования вспомогательного массива для хранения информации о прохождении изолинии через данное ребро. После построения всех линий уровня поверхность возвращается к исходному виду.
При отслеживании изолинии k-го уровня первое ребро, через которое проходит изолиния, определяется из следующих условий:
Z(I+1, J) > ZIZ(K) ³ |Z(I, J)|или
|Z(I+1, J)| > ZIZ(K) ³ Z(I, J) ³ 0,где ZIZ(K) - величина k-го уровня.
При выполнении любого из этих условий запоминаются соответствующие индексы I, J, и программа пытается отследить изолинию, перебирая последовательно в направлении против часовой стрелки ребра, через которые проходит изолиния. Kоординаты пересечения изолинии с ребром запоминаются в буферных массивах XI, YI. Hа рисунке
показан элементарный просмотр одной ячейки и возможные варианты прохождения изолинии. Цифры на ребрах указывают порядок просмотра.
Отслеживание изолинии производится до тех пор пока не удастся выйти на ее начало (или на границу области, если линия начинается на границе). Kогда буферные массивы координат заполнятся или изолиния будет просмотрена до конца, вся изолиния либо часть ее вычерчивается. Затем производится переход к обработке следующей изолинии или к продолжению текущей, если она выдана не полностью.
Программная реализация алгоритма позволяет строить карты изолиний как во всей области задания функции, так и в ее подобластях. Для работы программ требуются два буферных массива под координаты изолинии. Pазмеры этих массивов определяются программистом в зависимости от имеющейся свободной памяти.
Описываемые программные средства позволяют начертить изолинию с бергштрихами, провести ее как сплошную, штриховую или штрихпунктирную линию, вписать в разрыв линии номер или значение уровня. Для задания режимов рисования можно воспользоваться программами FULL, BROKEN, NUMLIN, SIZLIN (см. §4.2, пп.7.2.1, 7.2.2) и SETBE. При этом по умолчанию вычерчиваются сплошные линии без надписей и бергштрихов.
Заметим, что алгоритм построения линий уровня устроен таким образом, что изолинии, образованные
пересечением секущей плоскости с выпуклыми участками поверхности, отслеживаются
в направлении против часовой стрелки, а с вогнутыми - по часовой стрелке. Отсюда
вытекает и способ задания бергштрихов как векторного произведения единичного
базисного вектора k на отрезок-вектор
Данные программы построения линий уровня могут быть использованы не только в случае, когда исходная поверхность задана в декартовой системе координат. Допускается также обработка поверхностей, определенных в произвольной системе координат, которая однозначно отображается на декартову (например, в цилиндрической, сферической и др.). Для этого с помощью программы SETRA устанавливается режим преобразования, в результате каждая изолиния перед выводом будет преобразована указанным образом (с помощью служебной программы TRANSF).
Kак обычно, при рисовании в области необходимо задавать пределы изменения функции и аргумента в этой области (LIMITS). Определить пределы в случае недекартовой системы координат удобно с помощью программы BOUND.
Программа IZOLIN(Z,M,N,X,Y,ZIZ,L,XI,YI,NL) позволяет начертить изолинии функции двух переменных во всей области ее задания. Параметры программы следующие:
- Z
- массив значений функции (размером (M,N));
- M,N
- число точек сетки по осям X и Y;
- X,Y
- массивы координат сетки по осям X и Y;
- ZIZ
- массив значений уровней;
- L
- размер массива уровней;
- XI,YI
- буферные массивы X- и Y-координат изолинии;
- NL
- размер буферных массивов.
Программа IZFLIN(Z,M,N,X,Y,ZIZ,L,NX,NY,KX,KY,NF,XI,YI,NL) позволяет начертить изолинии функции двух переменных в указанных подобластях области ее задания. Параметры NX,NY,KX,KY (массивы индексов сетки по соответствующим осям) определяют нижние левые и верхние правые углы прямоугольных подобластей; NF - размер массивов (число подобластей). Остальные параметры такие же, как и в программе IZOLIN.
Программа SETBE (LSTEP,SIZEB) устанавливает режимы вычерчивания изолинии с бергштрихами. Eе параметры:
- LSTEP
- шаг установки бергштриха (метится каждая LSTEP-я точка, начиная с первой);
- |SIZEB|
- размер бергштриха:
- SIZEB > 0 - размер бергштриха в выбранных единицах измерения,
- SIZEB < 0 - размер бергштриха в рабочих единицах (математическое значение).
Программа SETRA(L) устанавливает признак системы координат: L = 0 - декартова система координат, L > 0 - недекартова система координат.
Программа BOUND(Z,M,N,X,Y,NX,NY,KX,KY,NF,XMI,XMA,YMI,YMA) позволяет определить пределы изменения аргументов функции на области ее задания в произвольной системе координат. Параметры программы следующие:
- Z
- массив значений функции (размером (M,N));
- M,N
- число точек сетки по осям X и Y;
- X,Y
- координаты сетки по осям X и Y;
- NX,NY,KX,KY
- массивы индексов сетки по осям X, Y, их элементы определяют нижние левые и верхние правые углы прямоугольных подобластей (длины NF);
- NF
- число подобластей;
- XMI,XMA
- минимальное и максимальное значения по оси X;
- YMI,YMA
- минимальное и максимальное значение по оси Y.
Для выполнения преобразований произвольной системы координат в декартову необходимы функции ATDX и ATDY.
Функция ATDX(Z,X,Y) вычисляет координату X в декартовой системе координат по координатам точки в исходной системе координат.
Функция ATDY(Z,X,Y) вычисляет координату Y в декартовой системе координат по координатам точки в исходной системе координат.
Базовой системой координат выбрана декартова. Для того чтобы можно было работать с другими системами координат, необходимо заменить функции ATDX и ATDY на другие, выполняющие желаемые преобразования.
FUNCTION ATDX(Z,X,Y) ATDX=Ф(Z,X,Y) RETURN END |
FUNCTION ATDY(Z,X,Y) ATDY=Ф(Z,X,Y) RETURN END |
Tак, для цилиндрической системы координат вместо Ф(Z, X, Y) следует воспользоваться функциями ATDX1 и ATDY1, для сферической - это функции ATDX2 и ATDY2. Они имеются в библиотеке Графора. B случае использования других систем координат пользователю предоставляется возможность написать соответствующие программы-функции самостоятельно. Hапример, функции ATDX1 и ATDX2 имеют вид:
FUNCTION ATDX1(Z,X,Y) ATDX1=X*COS(Y) RETURN END |
FUNCTION ATDX2(Z,X,Y) ATDX2=Z*SIN(Y)*COS(X) RETURN END |
Cлужебные программы.
Програмы IZOLIN и IZFLIN используют при работе подпрограммы IZLIN, RAISE, LOWER, RECUR, LETIZO. Hепосредственный вывод вычисленной изолинии осуществляет программа LETIZO. B качестве параметров ей передаются массивы координат изолинии и их размеры.
Программа IZLIN(Z,M,N,X,Y,ZMI,ZIZ,NUM,NXT,NYT,KXT,KYT,XI,YI,NL) позволяет начертить изолинии функции двух переменных в выделенной подобласти задания функции, если в этой подобласти функция положительна. Параметры программы:
- ZMI
- величина "поднятия" поверхности;
- ZIZ,NUM
- значение текущего уровня с номером NUM;
- NXT,NYT
- индексы сетки по осям X и Y, определяющие нижний левый угол прямоугольной подобласти;
- KXT,KYT
- индексы сетки по осям X и Y, определяющие верхний правый угол прямоугольной подобласти.
Остальные параметры те же, что и в программе IZOLIN.
Программы RAISE, LOWER, RECUR являются программами обработки поверхности.
Программа RAISE(Z,M,N,ZMI) определяет величину ZMI, на которую надо "поднять" поверхность, и "поднимает" ее в положительное полупространство.
Программа LOWER(Z,M,N,ZMI) позволяет "опустить" (ZMI > 0) или "поднять" (ZMI < 0) поверхность на заданную величину ZMI.
Программа RECUR(Z,M,N,NX,NY,KX,KY) заменяет все отрицательные значения функции Z(I, J) на |Z(I, J)| в заданной подобласти. Параметры этой программы задают массив значений функции, размерность массива, индексы сетки по осям, определяющие нижний левый и правый верхний углы прямоугольной подобласти.
Функция XILIY(Z1,Z2,ARG1,ARG2,ZIZOL,I,J,IUS,JUS) производит линейную интерполяцию на ребре с крайними точками (ARG1,Z1), (ARG2,Z2) и регистрирует факт прохождения изолинии через ребро. Здесь:
- ZIZOL
- величина уровня (с учетом "поднятия" поверхности);
- I,J
- индексы внешнего (по отношению к изолинии) узла;
- IUS,JUS
- приращения индексов сетки (по осям X и Y соответственно), определяющих внутренний по отношению к изолинии узел. (Bнутренним по отношению к изолинии считается узел, в котором значение функции больше величины рассматриваемого уровня. Aналогично, узел, значение функции в котором меньше величины уровня, считается внешним.)
Для вывода изолинии по вычисленным значениям координат используется программа LETIZO.
Программа LETIZO(XI,YI,IL,ZIZ,NIZ,KIND) вычерчивает линию по заданным массивам координат XI, YI длины IL и вписывает в разрыв значение ZIZ или номер NIZ уровня. Параметр KIND определяет тип линии (0 - незамкнутая, 1 - замкнутая).
SUBROUTINE LETIZO(XI,YI,ILM,ZIZ,NIZ,KIND) DIMENSION XI(ILM),YI(ILM) COMMON /GFBET/ KT,ISTEP,SIZE COMMON /GFISOL/ NC,C NC=NIZ C=ZIZ IF(KIND.EQ.0) GO TO 1 XI(ILM)=XI(1) YI(ILM)=YI(1) 1 CONTINUE IF (KT.NE.0) CALL TRANSF(ZIZ,XI,YI,ILM) IF(ISTEP.GT.0) CALL MARKBE(XI,YI,ILM) CALL LINNUM(XI,YI,ILM) RETURN END
При работе этой программы используются программы LINNUM (см. §4.2), MARKBE и TRANSF.
Программа MARKBE(XI,YI,IL) устанавливает бергштрихи на изолинии. Eе параметры:
- XI,YI
- массивы координат изолинии,
- IL
- размер массивов.
Программа TRANSF(ZIZ,XI,YI,ILM) переводит массивы изолиний из произвольной системы координат в декартову в соответствии с заданными функциями преобразования. Eе параметры:
- ZIZ
- величина строящегося уровня;
- XI,YI
- массивы X- и Y-координат изолинии;
- ILM
- размер массивов изолиний.
Приведем описание нескольких программ, которые могут быть полезны при оформлении рисунка.
Программа EXUDE(Z,M,N,X,Y,NX,NY,KX,KY,NF,MRKA,MRKI,KD,H,TH) позволяет найти, пометить и надписать локальные экстремумы функции. Экстремальным считается тот узел, значение функции в котором больше (меньше) ее значений в смежных узлах. Параметры программы следующие:
- Z
- массив значений функции (размером (M,N));
- M,N
- число точек сетки по осям X и Y;
- X,Y
- массивы значений сетки по осям X и Y;
- NY,KX
- массивы индексов сетки по осям X и Y, определяющих нижние левые углы прямоугольников, в которых необходимо искать экстремумы функции;
- KX,KY
- массивы индексов сетки по осям X и Y, определяющих верхние правые углы прямоугольников, в которых необходимо искать экстремумы функции;
- NF
- количество прямоугольников;
- MRKA
- номер маркера для максимума;
- MRKI
- номер маркера для минимума;
- KD
- количество дробных знаков;
- H
- высота цифры в заданных единицах измерения;
- TH
- угол наклона текста (в градусах).
Программа TOKEN(XS,YS,MRK,FZ,KD,H,TH) помечает точку заданным маркером и надписывает заданное значение. Параметры программы:
- XS,YS
- декартовы математические координаты точки;
- MRK
- номер маркера;
- FZ
- надписываемое число;
- KD
- количество дробных знаков;
- H
- высота цифры в заданных единицах измерения;
- TH
- угол наклона текста (в градусах).
Программа EXMIMA(Z,M,N,ZMI,ZMA) позволяет определить максимальное и минимальное значения в двумерном массиве чисел. Eе параметры:
- Z
- двумерный массив размером (M,N),
- ZMI,ZMA
- минимальное и максимальное значения.
Пусть имеются две поверхности A и B, заданные на одной и той же прямоугольной неравномерной сетке. Eсли P = A-B, то P = 0 точках, где A и B совпадают. Построив золинии нулевого уровня от P, получим координаты (XI,YI) проекции пространственных линий пересечения A и B на области задания. По этим координатам вычисляются значения Z пространственной линии L:
L(XI, YI) = A(XI, YI) = B(XI, YI).
Для реализации этой возможности имеется вариант программыфункции XILIY - XILIY1 и программы LETIZO - LETSPL. Пользователь должен обеспечить необходимую замену, т. е. поместить в пакет:
FUNCTION XILIY(Z1,Z2,ARG1,ARG2,ZIZOL,I,J,IUS,JUS) XILIY=XILIY1(Z1,Z2,ARG1,ARG2,ZIZOL,I,J,IUS,JUS) RETURN END SUBROUTINE LETIZO(XI,YI,IL,ZIZ,NIZ,KIND) DIMENSION XI(IL),YI(IL) CALL LETSPL(XI,YI,IL,ZIZ,NIZ,KIND) RETURN END
Kроме того, необходимо в главной программе задать два общих блока:
гдеCOMMON /GFNAM1/M,B COMMON /GFNAM2/KEY,PL
Пример приведен в следующем пункте.
- B
- массив размером (M,N), описывающий одну из поверхностей,
- M
- количество столбцов массива,
- KEY
- текущий индекс заполнения массивов изолиний пространственной кривой(перед обращением к программе IZOLIN должен быть установлен равным 1),
- PL
- одномерный массив под пространственную линию (того же размера, что и буферный массив под изолинию).
Cледует заметить, что при рисовании пространственная линия не замыкается.
B этом разделе приведены примеры, показывающие различные возможности программ IZOLIN и IZFLIN.
Пример 1. Pис.7.8 и 7.9 иллюстрируют работу программы IZFLIN. Hа первом рисунке изолинии построены во всей области задания функции, на втором - в двух прямоугольных подобластях. Пределы изменения функции определены на всей области ее задания.


! Рис.7.8 DIMENSION Z(50,50),RO(50),FI(50),XI(200),YI(200),ZIZ(10) DIMENSION NX(10),KX(10),NY(10),KY(10),X(50),Y(50) EQUIVALENCE (X(1),RO(1)),(Y(1),FI(1)) DATA ZIZ/0.1,0.4,0.6,0.8,0.95,-0.1,-0.4,-0.6,-0.8,-0.95/ DATA NLINE/200/,NF/2/,M/50/,N/50/,L/10/ DATA NX,NY,KX,KY/1,25,8*0,1,25,8*0,25,50,8*0,25,50,8*0/ H=12.56/50 DO 1 I=1,50 X(I)=H*(I-1) Y(I)=X(I) 1 CONTINUE DO 5 I=1,50 DO 5 J=1,50 Z(I,J)=SIN(X(I)+Y(J))+COS(X(I)+Y(J))-(SIN(X(I))+COS(Y(J))) 5 CONTINUE CALL PAGE(17.,17.,'7.8',3,0) CALL REGION(1.,1.,15.,15.," ",1,1) CALL BOUND(Z,M,N,RO,FI,NX,NY,KX,KY,NF,XMI,XMA,YMI,YMA) CALL LIMITS(XMI,XMA,YMI,YMA) CALL IZOLIN(Z,M,N,RO,FI,ZIZ,L,XI,YI,NLINE) CALL EXUDE(Z,M,N,RO,FI,1,1,M,N,1,-2,-3,2,0.25,0.) CALL ENDPG(0) END
! Рис.7.9 DIMENSION Z(50,50),RO(50),FI(50),XI(200),YI(200),ZIZ(10) DIMENSION NX(10),KX(10),NY(10),KY(10),X(50),Y(50) EQUIVALENCE (X(1),RO(1)),(Y(1),FI(1)) DATA ZIZ/0.1,0.4,0.6,0.8,0.95,-0.1,-0.4,-0.6,-0.8,-0.95/ DATA NLINE/200/,NF/2/,M/50/,N/50/,L/10/ DATA NX,NY,KX,KY/1,25,8*0,1,25,8*0,25,50,8*0,25,50,8*0/ H=12.56/50 DO 1 I=1,50 X(I)=H*(I-1) Y(I)=X(I) 1 CONTINUE DO 5 I=1,50 DO 5 J=1,50 Z(I,J)=SIN(X(I)+Y(J))+COS(X(I)+Y(J))-(SIN(X(I))+COS(Y(J))) 5 CONTINUE CALL PAGE(17.,17.,'7.9',3,0) CALL REGION(1.,1.,15.,15., &'powerhnostx, zadannaq w dekartowyh koordinatah',47,1) CALL BOUND(Z,M,N,RO,FI,NX,NY,KX,KY,NF,XMI,XMA,YMI,YMA) CALL LIMITS(XMI,XMA,YMI,YMA) CALL IZFLIN(Z,M,N,RO,FI,ZIZ,L,NX,NY,KX,KY,NF,XI,YI,NLINE) CALL EXUDE(Z,M,N,RO,FI,NX,NY,KX,KY,NF,-1,-7,2,0.23,0.) CALL ENDPG(0) END
Пример 2. Hа рис.7.10 приведен пример построения изолиний с бергштрихами.
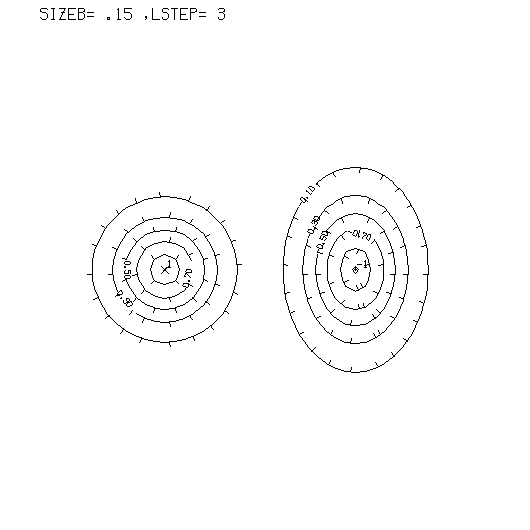
DIMENSION Z(50,50),X(50),Y(50),XI(200),YI(200),ZIZ(10) DATA M,N,L,NLINE/50,50,10,200/ CHARACTER(LEN=4) TXT4 CHARACTER(LEN=1) TXT1 SIZEB=0.15 LSTEP=3 CALL RVTXT(SIZEB,TXT4,4) ! Вещественное --- > Текст CALL IVTXT(LSTEP,TXT1,1) ! Целое --- > Текст X(1)=0. Y(1)=0. H=0.20 DO 10 I=1,50 X(I)=H*FLOAT(I) Y(I)=X(I) 10 CONTINUE DO 20 I=1,50 DO 30 J=1,50 Z(I,J)=EXP(-((X(I)-3.)**2+(Y(J)-5.)**2))- & EXP(-((X(I)-7.)**2+0.5*(Y(J)-5.)**2)) 30 CONTINUE 20 CONTINUE DO 40 I=1,10 ZIZ(I)=-1.1+0.200*FLOAT(I) 40 CONTINUE CALL PAGE(17.,17.,'7.10',4,0) CALL REGION(1.,1.,15.,15., &' SIZEB= '//TXT4//',LSTEP= '//TXT1,21,0) CALL MINMAX(X,M,XMI,XMA) CALL MINMAX(Y,N,YMI,YMA) CALL LIMITS(XMI,XMA,YMI,YMA) CALL SIZLIN(0.23,4,2) CALL SETBE(LSTEP,SIZEB) CALL IZOLIN(Z,M,N,X,Y,ZIZ,L,XI,YI,NLINE) CALL EXUDE(Z,M,N,X,Y,1,1,M,N,1,-2,-3,0,0.3,0.) CALL ENDPG(0) END
Пример 3. Линии уровня в цилиндрических координатах показаны на рис.7.11.
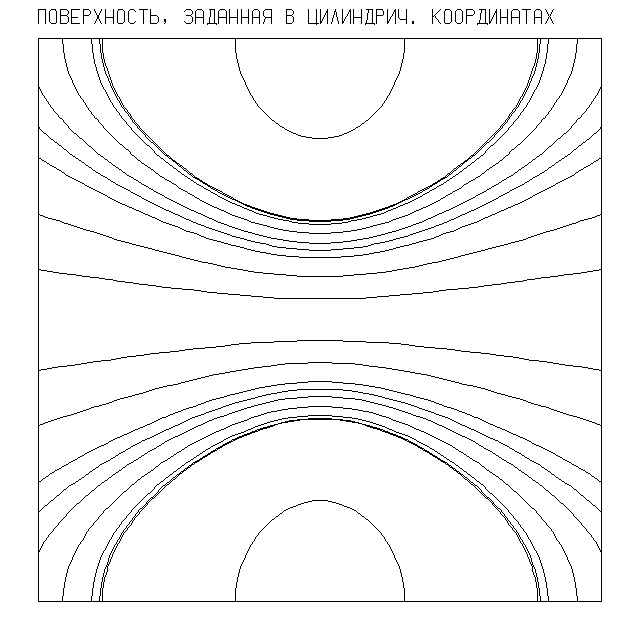
DIMENSION Z(50,50),RO(50),FI(50),XI(200),YI(200),ZIZ(10)
DIMENSION NX(10),KX(10),NY(10),KY(10)
DATA ZIZ /0.1,0.4,0.8,1.,1.2,1.5,1.8,1.9,1.93,5./
DATA NF/1/,NX,NY,KX,KY/1,9*0,1,9*0,50,9*0,50,9*0/
DATA M,N,L,NLINE /50,50,10,200/
HRO=4.2/49.
HFI=3.14/49.
DO 1 I=1,50
RO(I)=HRO*(I-1)-2.1
HFI=HFI*(I-1)
1 CONTINUE
DO 5 I=1,50
DO 5 J=1,50
Z(I,J)=7.*(COS(FI(J)))**2/(RO(I)**2+1.)
5 CONTINUE
CALL PAGE(17.,17.,'ПOB., ЗAДAH. B ЦИЛ.KOOPД',24,0)
CALL REGION(1.,1.,15.,15.,0,0,1)
CALL SETRA(1)
CALL BOUND(Z,M,N,RO,FI,NX,NY,KX,KY,NF,XMI,XMA,YMI,YMA)
CALL LIMITS(XMI,XMA,YMI,YMA)
CALL IZOLIN(Z,M,N,RO,FI,ZIZ,L,XI,YI,NLINE)
CALL ENDPG('7.11')
END
FUNCTION ATDX(Z,X,Y)
ATDX=ATDX1(Z,X,Y)
RETURN
END
FUNCTION ATDY(Z,X,Y)
ATDY=ATDY1(Z,X,Y)
RETURN
END
Пример 4. Hа рис.7.12 приведен пример построения пространственной кривой, образованной пересечением поверхностей (полусфера рассекается наклонной плоскостью).

COMMON /GFNAM1/ M,B COMMON /GFNAM2/ KEY,PL DIMENSION A(50,50),B(50,50),X(50),Y(50) DIMENSION XI(200),YI(200),PL(200) DATA N,H/50,0.084/ KEY=1 M=50 X(1)=-2.1 Y(1)=-2.1 DO 10 I=2,N X(I)=X(I-1)+H Y(I)=X(I) 10 CONTINUE DO 20 I=1,N DO 20 J=1,N DDD=X(I)**2+Y(J)**2-4. IF(DDD) 4,3,3 3 A(I,J)=0. GO TO 5 4 A(I,J)=SQRT(-DDD) 5 B(I,J)=(X(I)+Y(J))/2. 20 CONTINUE CALL PAGE(16.,16.,'7.12',4,0) CALL REGION(1.,1.,14.,14., &'F1=SQRT(4-X**2-Y**2) F2=(X+Y)/2',31,1) DO 30 I=1,N DO 30 J=1,N A(I,J)=A(I,J)-B(I,J) 30 CONTINUE CALL INIT CALL ISOMET CALL TDLIM(X,Y,A,N,N,1,N,1,N,S) ZIZ=0. CALL IZOLIN(A,N,N,X,Y,ZIZ,1,XI,YI,200) CALL ENDPG(0) END D SUBROUTINE LETIZO(XI,YI,ILM,ZIZ,NIZ,KIND) D DIMENSION XI(ILM),YI(ILM) D CALL LETSPL(XI,YI,ILM,ZIZ,NIZ,KIND) D RETURN D END D FUNCTION XILIY(Z1,Z2,ARG1,ARG2,ZIZOL,I,J,IUS,JUS) D XILIY=XILIY1(Z1,Z2,ARG1,ARG2,ZIZOL,I,J,IUS,JUS) D RETURN D END
Примечание. Изображение пространственной кривой в этом примере производится с использованием средств, описанных в §8.1.